如图所示，电源电动势E＝10V，内电阻r＝0.5Ω，R1＝5.5Ω，R2＝4Ω，水平放置的平行板电容器的电容C＝5×10－5 F，当开关S闭合后，求：
（1）流过R1的电流I和路端电压U；
（2）电源消耗的总功率P和R2上消耗的功率P2；
（3）电容器所带的电量Q。
如图所示，间距
的足够长的光滑平行金属导轨与水平面成
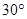角放置，导轨电阻不计，导轨上端连有
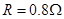的电阻，磁感应强度为
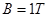的匀强磁场垂直导轨平面向上，
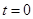时刻有一质量
，电阻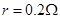
的金属棒，以
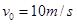的初速度从导轨上某一位置
开始沿导轨向上滑行，金属棒垂直导轨且与导轨接触良好，与此同时对金属棒施加一个沿斜面向上且垂直于金属棒的外力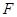
，使金属棒做加速度大小为
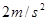的匀减速直线运动，则：
（1）
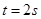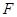时，外力的大小？
（2）若已知金属棒运动从开始运动到最高点的过程中，电阻
上产生的热量为
，求此过程中外力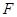做的功？
（3）到最高点后，撤去外力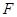，经过足够长时间后，最终电阻上消耗的功率是多少？
如图18所示，在xOy平面内某介质中有一列波源位于O点沿x 轴正方向传播的简谐横波，在t=0时，P点（x=20cm处）位于波峰，t=1s时，P点位于平衡位置，且速度方向向下，Q点（x=80cm处）位于平衡位置下方的最大位移处。已知此波的振幅
，波长
，周期
求：
（1）画出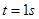
时，PQ之间的波形图（把图画在答题卷的相应位置）
（2）该波在介质中的波速
（3）在图19中画出波源O点的振动图像（把图画在答题卷的相应位置）
如图17所示，一半径为R的
透明圆柱体放在水平面上，AOB为透明圆柱体的截面，一束蓝光从AO面的中点沿水平方向射入透明体，经AB弧面折射后，光线射到水平面上的P点，测得OP距离为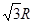
，则：
（1）画出光路图，并求出透明圆柱体对蓝光的折射率
（2）蓝光从AO面射入到P点的总时间（设空气中光速为c）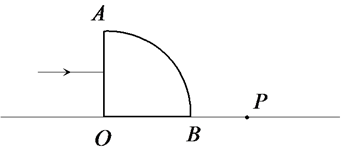
图17
为确定爱因斯坦的质能方程
的正确性，设计了如下实验：用动能为
MeV的质子轰击静止的锂核
Li，生成两个
粒子，测得两个粒子的动能之和为
MeV。
（1）写出该反应方程。
（2）通过计算说明正确。（已知质子、粒子、锂核的质量分别取
、
、
，1u相当于931.5MeV）
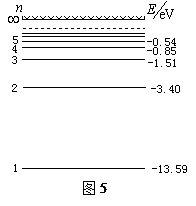
如图5所示为氢原子能级示意图，现有每个电子的动能都是Ee=12.89eV的电子束与处在基态的氢原子束射入同一区域，使电子与氢原子发生正碰。已知碰撞前一个电子和一个氢原子的总动量恰好为零。碰撞后氢原子受激发，跃迁到n＝4的能级。求碰撞后电子和受激氢原子的总动能。已知电子的质量me与氢原子的质量mH之比为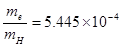
。