示波器是一种多功能电学仪器,可以在荧光屏上显示出被检测的电压波形.它的工作原理等效成下列情况:如图所示,真空室中电极K发出电子(初速度不计),经过电压为U1的加速电场后,由小孔S沿水平金属板,A、B间的中心线射入板中.板长L,相距为d,在两板间加上如图乙所示的正弦交变电压,前半个周期内B板的电势高于A板的电势,电场全部集中在两板之间,且分布均匀.在每个电子通过极板的极短时间内,电场视作恒定的.在两极板右侧且与极板右端相距D处有一个与两板中心线垂直的荧光屏,中心线正好与屏上坐标原点相交.当第一个电子到达坐标原点O时,使屏以速度v沿-x方向运动,每经过一定的时间后,在一个极短时间内它又跳回到初始位置,然后重新做同样的匀速运动.(已知电子的质量为m,带电量为e,不计电子重力)求: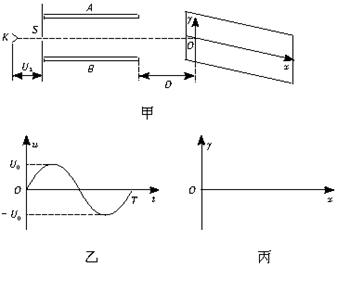
(1)电子进入AB板时的初速度;
(2)要使所有的电子都能打在荧光屏上,图乙中电压的最大值U0需满足什么条件?
(3)要使荧光屏上始终显示一个完整的波形,①荧光屏必须每隔多长时间回到初始位置?②计算这个波形的最大峰值和长度.③并在如图丙所示的x-y坐标系中画出这个波形.
(1)根据玻尔原子结构理论,氦离子( )的能级图如图所示。电子处在n=5轨道上比处在n=3轨道上离氦核的距离_______ (选填“近”或“远”)。当大量
)的能级图如图所示。电子处在n=5轨道上比处在n=3轨道上离氦核的距离_______ (选填“近”或“远”)。当大量 处在n=3的激发态时,由于跃迁所发射的谱线有_______条。
处在n=3的激发态时,由于跃迁所发射的谱线有_______条。
(2)如图所示,一质量为M、长为l的长方形木板B放在光滑的水平地面上,在其右端放一质量为m的小木块A,m<M。现以地面为参照系,给A和B以大小相等、方向相反的初速度,使A开始向左运动、B开始向右运动,但最后A刚好没有滑离木板。以地面为参照系。
(1)若已知A和B的初速度大小为v0,求它们最后的速度的大小和方向。
(2)若初速度的大小未知,求小木块A向左运动到达的最远处(从地面上看)离出发点的距离。
如图所示,A、B两板间距为d1=0.04 m,板间电势差为U1=2×103V,C、D两板间距离d2=0.40m,C、D两板板长均为L=1.0 m,两板间加一恒定电压U2(C板电势高)。在S处有一电量为q=8×10-5C、质量为m=2×10-6C的带正电粒子,无初速释放,经A、B间电场加速又经C、D间电场偏转后直接进入一个垂直纸面向里的匀强磁场区域,磁感强度为B=100 T,不计重力影响。欲使该带电粒子经过磁场偏转后,飞回C、D两板间,恰打在D板的左边缘。求: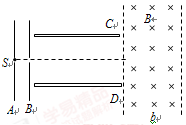
(1)该带电粒子以多大的初速度飞入C、D两板间?
(2)C、D两板间电势差U2
(3)匀强磁场的宽度b至少为多少?
如图所示,在高速公路某处安装了一台500万像素的固定雷达测速仪,可以准确抓拍超速车辆以及测量运动车辆的加速度.若B为测速仪,A为汽车,两者相距355 m,此时刻B发出超声波,同时A由于紧急情况而急刹车,当B接收到反射回来的超声波信号时,A恰好停止,且此时A、B相距335 m,已知声速为340 m/s。
(1)求汽车刹车过程中的加速度;
(2)若该路段汽车正常行驶时速度要求在60km/h~110km/h,则该汽车刹车前的行驶速度是否合法?
如图所示,某传送带与地面倾角θ=37o,AB之间距离L1=2.05m,传送带以v0=1.0m/s的速率逆时针转动。质量为M=1.0kg,长度L2=1.0m的木板上表面与小物块的动摩擦因数μ2=0.4,下表面与水平地面间的动摩擦因数μ3=0.1,开始时长木板靠近传送带B端并处于静止状态。现在传送带上端A无初速地放一个不计大小、质量为m=1.0kg的小物块,它与传送带之间的动摩擦因数为μ1=0.5,假设物块在滑离传送带至木板右端时速率不变,sin37o=0.6,cos37 o =0.8, g=10m/s2。求: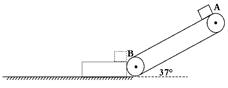
(1)物块离开B点的速度大小;
(2)物块在木板上滑过的距离;
(3)木板在地面上能滑过的最大距离。
如图所示,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间距离为L。已知A、B的中心和O三点始终共线,A和B分别在O的两侧。引力常数为G。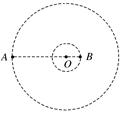
(1)求两星球做圆周运动的周期;
(2)在地月系统中,若忽略其他星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为T1。但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期记为T2。已知地球和月球的质量分别为5.98×1024 kg和7.35 ×1022 kg。求T2与T1两者平方之比。(结果保留三位小数)