（本小题满分12分）
如图，已知多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AC=AD=CD=DE=2，AB=1，F为CD的中点．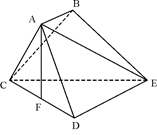
（Ⅰ）求证：AF⊥平面CDE；
（Ⅱ）求面ACD和面BCE所成锐二面角的大小．
如图，某观测站C在城A的南偏西
的方向，从城A出发有一条走向为南偏东
的公路，在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去，行驶了20km后到达D处，测得C，D两处的距离为21km，这时此车距离A城多少千米？
已知函数
（1）求函数
的最小正周期和单调增区间；
（2）作出函数在一个周期内的图象。
关于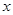
的不等式
，其中
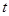是实参数.
（1）当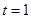
时，解上面的不等式.
(2)若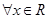
，上面的不等式均成立，求实数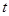的范围.
以坐标原点为极点，横轴的正半轴为极轴的极坐标系下，有曲线C：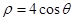
，过极点的直线
（
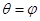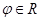且
是参数）交曲线C于两点0，A，令OA的中点为M.
(1)求点M在此极坐标下的轨迹方程（极坐标形式）.
(2)当
时，求M点的直角坐标.
如图，
的外接圆的切线
与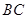
的延长线交于点
，
的平分线与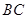交于点D.
(1)求证：
(2)若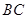是的外接圆的直径，且
，
＝1.求
长.