如图,D、E分别是AC,AB上的点,∠ADE=∠B,AG⊥BC于点G,AF⊥DE于点F.若AD=3,AB=5,求: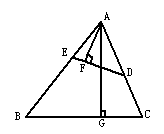
(1) ;
;
(2)△ADE与△ABC的周长之比;
(3)△ADE与△ABC的面积之比.
两个城镇A、B与两条公路l1、l2位置如图所示,电信部门需在C处修建一座信号反射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路l1,l2的距离也必须相等,那么点C应选在何处?请在图中,用尺规作图找出所有符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
AB是⊙O的直径,AD与⊙O相交,点C是⊙O上一点,经过点C的直线交AD于点E.
(1)如图1 ,若AC平分∠BAD,CE⊥AD于点E,求证:CE是⊙O的切线;
(2)如图2,若CE是⊙O的切线,CE⊥AD于点E,AC是∠BAD的平分线吗?说明理由;
(3)如图3,若CE是⊙O的切线,AC平分∠BAD,AB=8,AC=6,求AE的长度.
已知关于x的一元二次方程k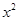 -(4k+1)x+3k+3=0.
-(4k+1)x+3k+3=0.
(1)试说明:无论k取何值,方程总有两个实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5.当△ABC是等腰三角形时,求k的值.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.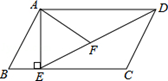
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6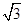 ,AF=4
,AF=4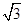 ,求sinB的值.
,求sinB的值.
如图,四边形ABCD内接于⊙O,BC是直径,∠BAD=120°,AB=AD.
(1)求证:四边形ABCD是等腰梯形;
(2)已知AC=6,求阴影部分的面积.