如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.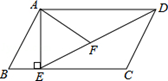
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6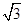 ,AF=4
,AF=4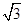 ,求sinB的值.
,求sinB的值.
如图,抛物线 经过 , 两点,交 轴于点 ,点 为抛物线的顶点,连接 ,点 为 的中点.请解答下列问题:
(1)求抛物线的解析式及顶点 的坐标;
(2)在 轴上找一点 ,使 的值最小,则 的最小值为 .
(注:抛物线 的对称轴是直线 ,顶点坐标为 ,

如图,在 中, , 于 .求证: .

已知:在平面直角坐标系中,点 为坐标原点,点 在 轴的负半轴上,直线 与 轴、 轴分别交于 、 两点,四边形 为菱形.
(1)如图1,求点 的坐标;
(2)如图2,连接 ,点 为 内一点,连接 、 , 与 交于点 ,且 ,点 在线段 上,点 在线段 上,且 ,连接 、 ,若 ,求 的值;
(3)如图3,在(2)的条件下,当 时,求点 的坐标.

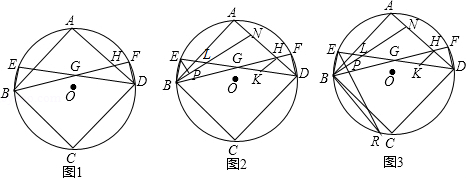
已知: 是正方形 的外接圆,点 在 上,连接 、 ,点 在 上连接 、 , 与 、 分别交于点 、点 ,且 平分 .
(1)如图1,求证: ;
(2)如图2,在线段 上取一点 (点 不与点 、点 重合),连接 交 于点 ,过点 作 交 于点 ,过点 作 ,垂足为点 ,当 时,求证: ;
(3)如图3,在(2)的条件下,当 时,延长 交 于点 ,连接 ,若 的面积与 的面积的差为 ,求线段 的长.
春平中学要为学校科技活动小组提供实验器材,计划购买 型、 型两种型号的放大镜.若购买8个 型放大镜和5个 型放大镜需用220元;若购买4个 型放大镜和6个 型放大镜需用152元.
(1)求每个 型放大镜和每个 型放大镜各多少元;
(2)春平中学决定购买 型放大镜和 型放大镜共75个,总费用不超过1180元,那么最多可以购买多少个 型放大镜?