阅读下面的材料：
小明在学习中遇到这样一个问题：若1≤x≤m，求二次函数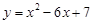
的最大值．他画图研究后发现，
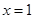和
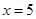时的函数值相等，于是他认为需要对
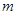进行分类讨论．
他的解答过程如下：
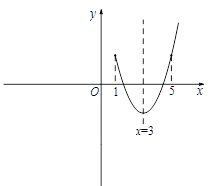
∵二次函数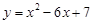的对称轴为直线
，
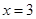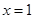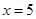∴由对称性可知，和时的函数值相等．
∴若1≤m＜5，则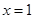时，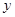
的最大值为2；
若m≥5，则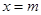
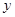时，的最大值为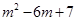
．
请你参考小明的思路，解答下列问题：
（1）当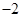
≤x≤4时，二次函数
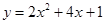的最大值为_______；
（2）若p≤x≤2，求二次函数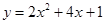的最大值；
（3）若t≤x≤t+2时，二次函数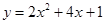的最大值为31，则
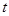的值为_______．
在数轴上把下列各数表示出来，并用“＜”连接各数。（共4分）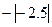
，
，
，
，
，
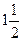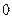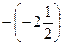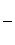
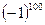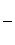
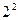
（本题4分）
把下列各数填在相应的大括号里：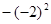
，
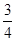，0.86，
，
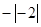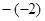，0，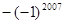
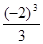
负整数集合：（…）；
负分数集合：（…）；
正分数集合：（…）；
非负有理数集合（…）。
【阅读】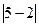 
表示5与2差的绝对值，也可理解为5与2两数在数轴上所
对应的两点之间的距离；
可以看做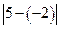
，表示5与－2的差的绝对值，也
可理解为5与－2两数在数轴上所对应的两点之间的距离．
【探索】
(1) =___________．
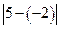(2) 利用数轴，找出所有符合条件的整数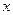
，使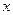所表示的点到5和—2的距离之和为7
(3) 由以上探索猜想，对于任何有理数，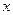
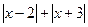是否有最小值? 如果有，写出最
小值；如果没有，说明理由
用火柴棒按下图方式搭三角形．
(1)填写下表：
(2)照这样的规律搭下去，搭n个这样的三角形需要根火柴棒。
小王上周五在股市以收盘价每股25元买进某公司的股票1000股，在接下来的一周交易日内，他记下该股票每日收盘价比前一天的涨跌情况(单位：元)：
| 星期 |
一 |
二 |
三 |
四 |
五 |
| 每股涨跌 |
＋2 |
－0．5 |
＋1．5 |
－1．8 |
＋0．8 |
(1)星期二收盘时，该股票每股多少元?
(2)本周内，该股票收盘时的最高价、最低价分别是多少?
(3)已知买入股票与卖出股票均需支付成交金额的0.15%的交易费，若小王在本周五以收盘价将全部股票卖出，他的收益情况如何?