(本小题共12分)
已知△ABC的角A,B,C的对边依次为a,b,c,若满足 ,
,
(1)求∠C大小;
(2)若c=2,且△ABC为锐角三角形,求a+b取值范围。
如图,在四棱锥 中,底面 四边长为1的 菱形, , 底面 , , 为 的中点.
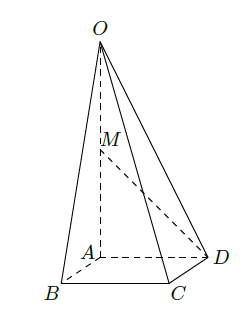
(Ⅰ)求异面直线
与
所成角的大小;
(Ⅱ)求点
到平面
的距离.
在某次普通话测试中,为测试汉字发音水平,设置了10张卡片,每张卡片印有一个汉字的拼音,其中恰有3张卡片上的拼音带有后鼻音"
".
(Ⅰ)现对三位被测试者先后进行测试,第一位被测试者从这10张卡片总随机抽取1张,测试后放回,余下2位的测试,也按同样的方法进行.求这三位被测试者抽取的卡片上,拼音都带有后鼻音"
"的概率。
(Ⅱ)若某位被测试者从10张卡片中一次随机抽取3张,求这三张卡片上,拼音带有后鼻音"
"的卡片不少于2张的概率.
已知函数
(Ⅰ)求函数
的最小正周期和图象的对称轴方程
(Ⅱ)求函数
在区间
上的值域
(本小题满分13分)
对于各项均为整数的数列 ,如果
,如果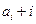 (
( =1,2,3,…)为完全平方数,则称数
=1,2,3,…)为完全平方数,则称数
列 具有“
具有“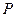 性质”。
性质”。
不论数列 是否
是否 具有“
具有“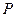 性质”,如果存在与
性质”,如果存在与 不是同一数列的
不是同一数列的 ,且
,且 同
同
时满足下面两个条件:① 是
是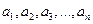 的一个排列
的一个排列 ;②数列
;②数列 具有“
具有“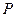 性质”,则称数列
性质”,则称数列 具有“变换
具有“变换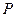 性质”。
性质”。
(I)设数列 的前
的前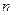 项和
项和 ,证明数列
,证明数列 具有“
具有“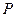 性质”;
性质”;
(II)试判断数列1,2,3,4,5和数列1,2,3,…,11是否具有“变换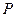 性质”,具有此性质的数列请写出相应的数列
性质”,具有此性质的数列请写出相应的数列 ,不具此性质的说明理由;
,不具此性质的说明理由;
(III)对于有限项数列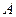 :1,2,3,…,
:1,2,3,…,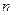 ,某人已经验证当
,某人已经验证当 时,
时,
数列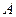 具有“变换
具有“变换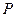 性质”,试证明:当”
性质”,试证明:当”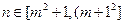 时,数
时,数 列
列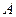 也具有“变换
也具有“变换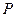 性质”。
性质”。
(本小题满分14分)
已知 函数,其中
函数,其中 ,其中
,其中 。
。
(I)求函数 的零点;
的零点;
(II)讨论 在区间
在区间 上的单调性;
上的单调性;
(III)在区间 上,
上, 是否存在最小值?若存在,求出最小值;若不存在,请说明理由。
是否存在最小值?若存在,求出最小值;若不存在,请说明理由。