在边长为a的正方形中挖去一个边长为a的小正方形(a>b)(如图),把余下的部分拼成一个矩形(如图),根据两个图形中阴影部分的面积相等,可以验证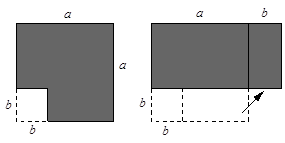
A. |
B. |
C. |
D.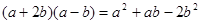 |
2的相反数是
A.2 B.-2 C. D.
A.2 B.-2 C. D.
如图,是由8个相同的小立方块搭成的几何体的左视图,它的三个视图是2×2的正方形.若拿掉若干个小立方块后(几何体不倒掉),其三个视图仍都为2×2的正方形,则最多能拿掉小立方块的个数为
| A.1 | B.2 | C.3 | D.4 |
在正五边形ABCDE中,对角线AD,AC与EB分别相交于点M,N.下列结论错误的是
| A.四边形EDCN是菱形 | B.四边形MNCD是等腰梯形 |
| C.△AEM与△CBN相似 | D.△AEN与△EDM全等 |
已知抛一枚均匀硬币正面朝上的概率为,下列说法错误的是
| A.连续抛一均匀硬币2次必有1次正面朝上 |
| B.连续抛一均匀硬币10次都可能正面朝上 |
| C.大量反复抛一均匀硬币,平均100次出现正面朝上50次 |
| D.通过抛一均匀硬币确定谁先发球的比赛规则是公平的 |
小华在电话中问小明:“已知一个三角形三边长分别是4,9,12,如何求这个三角形的面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形正确的是