已知抛物线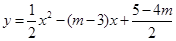 .
.
(1) 求证:无论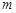 为任何实数,抛物线与
为任何实数,抛物线与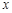 轴总有两个交点;
轴总有两个交点;
(2) 若A 、B
、B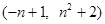 是抛物线上的两个不同点,求抛物线的解析式和
是抛物线上的两个不同点,求抛物线的解析式和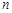 的值;
的值;
(3) 若反比例函数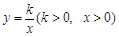 的图象与(2)中的抛物线在第一象限内的交点的横坐标为
的图象与(2)中的抛物线在第一象限内的交点的横坐标为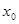 ,且满足2<
,且满足2<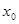 <3,求k的取值范围.
<3,求k的取值范围.
如图,在平面直角坐标系中,直线 与抛物线
与抛物线 交于A、B两点,点A在x轴上,点B的横坐标为-8.
交于A、B两点,点A在x轴上,点B的横坐标为-8.
(1)求该抛物线的解析式;
(2)点P是直线AB上方的抛物线上一动点(不与点A、B重合),过点P作x轴的垂线,垂足为C,交直线AB于点D,作PE⊥AB于点E.
①设△PDE的周长为l,点P的横坐标为x,求l关于x的函数关系式,并求出l的最大值;
②连接PA,以PA为边作图示一侧的正方形APFG.随着点P的运动,正方形的大小、位置也随之改变.当顶点F或G恰好落在y轴上时,直接写出对应的点P的坐标.
一透明的敞口正方体容器ABCD -A′B′C′D′ 装有一些液体,棱AB始终在水平桌面上,容器底部的倾斜角为α(∠CBE = α,如图17-1所示).
探究 如图1,液面刚好过棱CD,并与棱BB′ 交于点Q,此时液体的形状为直三棱柱,其三视图及尺寸如图2所示.解决问题:
(1)CQ与BE的位置关系是______,BQ的长是_______dm;
(2)求液体的体积;(参考算法:直棱柱体积V液 = 底面积SBCQ×高AB)
(3)求α的度数.(注:sin49°=cos41°= ,tan37°=
,tan37°= )
)
拓展 在图17-1的基础上,以棱AB为轴将容器向左或向右旋转,但不能使液体溢出,图17-3或图17-4是其正面示意图.若液面与棱C′C或CB交于点P,设PC = x,BQ = y.分别就图17-3和图17-4求y与x的函数关系式,并写出相应的α的范围.
延伸 在图17-4的基础上,于容器底部正中间位置,嵌入一平行于侧面的长方形隔板(厚度忽略不计),得到图17-5,隔板高NM =" 1" dm,BM = CM,NM⊥BC.继续向右缓慢旋转,当α = 60°时,通过计算,判断溢出容器的液体能否达到4 dm3.
等腰△ABC中,AB=AC,边AB绕点A逆时针旋转角度m得到线段AD.
(1)如图1,若∠BAC=30°,30°<m<180°,连接BD,请用含m的式子表示∠DBC的度数;
(2)如图2,若∠BAC=60°,0°<m<360°,连接BD,DC,直接写出△BDC为等腰三角形时m所有可能的取值_____;
(3)如图3,若∠BAC=90°,射线AD与直线BC相交于点E,是否存在旋转角度m,使 ,若存在,求出所有符合条件的m的值,若不存在,请说明理由.
,若存在,求出所有符合条件的m的值,若不存在,请说明理由.
小明早晨从家里出发匀速步行去上学,小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.已知小明在整个上学途中,他出发后分钟时,他所在的位置与家的距离为 千米,且
千米,且 与之间的函数关系的图像如图中的折线段
与之间的函数关系的图像如图中的折线段 所示.
所示.
(1)试求折线段 所对应的函数关系式;
所对应的函数关系式;
(2)请解释图中线段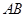 的实际意义;
的实际意义;
(3)请在所给的图中画出小明的妈妈在追赶小明的过程中,她所在位置与家的距离 (千米)与小明出发后的时间(分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)
(千米)与小明出发后的时间(分钟)之间函数关系的图像.(友情提醒:请对画出的图像用数据作适当的标注)
如图,AB为的直径,点C在⊙O上,点P是直径AB上的一点(不与A,B重合),过点P作AB的垂线交BC的延长线于点Q.
(1)在线段PQ上取一点D,使DQ=DC,连接DC,试判断CD与⊙O的位置关系,并说明理由.
(2)若cosB= ,BP=6,AP=1,求QC的长.
,BP=6,AP=1,求QC的长.