如图，在平面直角坐标系中，直线
与抛物线
交于A、B两点，点A在x轴上，点B的横坐标为－8.
（1）求该抛物线的解析式；
（2）点P是直线AB上方的抛物线上一动点（不与点A、B重合），过点P作x轴的垂线，垂足为C，交直线AB于点D，作PE⊥AB于点E.
①设△PDE的周长为l，点P的横坐标为x，求l关于x的函数关系式，并求出l的最大值；
②连接PA，以PA为边作图示一侧的正方形APFG．随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标．
如图1，四边形ABCD，AEFG都是正方形，E、G分别在AB、AD边上，已知AB=4．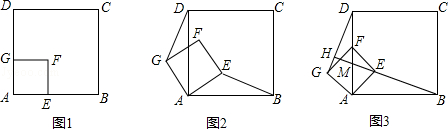
（1）求正方形ABCD的周长；
（2）将正方形AEFG绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，求证：BE=DG．
（3）将正方形AEFG绕点A逆时针旋转45°时，如图3，延长BE交DG于点H，设BH与AD的交点为M．
①求证：BH⊥DG；
②当AE=
时，求线段BH的长（精确到0．1）．
已知正比例函数y=x和反比例函数
的图象都经过点A（3，3）．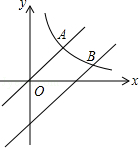
（1）直接写出反比例函数的解析式；
（2）把直线OA向下平移后与反比例函数的图象交于点B（6，m），求平移的距离．
已知一次函数y=kx+b的图象经过点（1，3）和点（2，5），求k和b的值．
如图，已知△ABC．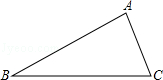
（1）作边BC的垂直平分线；
（2）作∠C的平分线．（要求：不写作法，保留作图痕迹）
①计算：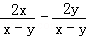
②解方程：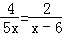
．