如图1，四边形ABCD，AEFG都是正方形，E、G分别在AB、AD边上，已知AB=4．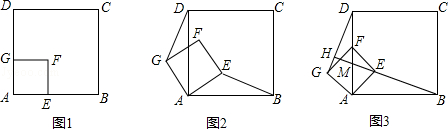
（1）求正方形ABCD的周长；
（2）将正方形AEFG绕点A逆时针旋转θ（0°＜θ＜90°）时，如图2，求证：BE=DG．
（3）将正方形AEFG绕点A逆时针旋转45°时，如图3，延长BE交DG于点H，设BH与AD的交点为M．
①求证：BH⊥DG；
②当AE=
时，求线段BH的长（精确到0．1）．
（本小题满分8分）如图，P是等边三角形ABC内的一点，连结PA，PB，PC，以BP为边作∠PBQ=60°，且BP=BQ，连结CQ．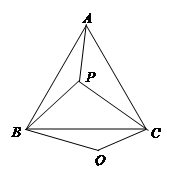
(1)观察并猜想AP与CQ之间的大小关系，并说明理由．
(2)若PA=3，PB=4，PC=5，连结PQ，判断△PQC的形状并说明理由．
（本小题满分8分）如图，已知AE∥BC，AE平分∠DAC．求证：AB=AC．
（本小题满分6分）如图，已知AB∥CD，若∠A=20°，∠E=35°，求∠C．
（本小题满分6分）解不等式组：
，并在数轴上表示出不等式组的解集．
（本题9分）平安加气站某日7：00前的储气量为10000立方米．加气站在加气过程中每把加气枪均以每小时200立方米的速度为汽车加气．设加气站从7：00开始，加气时间为x（小时）（加气期间关闭加气枪的时间忽略不计）．另外，加气站在不同时间段加气枪的使用数量如下：
（1）7：30时加气站的储气量为立方米；
（2）当x＞1时，试用含x的代数式表示加气站加气x小时后的储气量（答案要求化简）；
（3）若每辆车的加气量均为20立方米，试说明前70辆车能否在当天8：30
之前加完气？若能，请加以说明；若不能，则8：00以后还需添加几把枪加气才能保证在当天8：30恰好加完气？