如图，抛物线y＝
x2－
x－12与x轴交于A、C两点，与y轴交于B点．
（1）求△AOB的外接圆的面积；
（2）若动点P从点A出发，以每秒2个单位沿射线AC方向运动；同时，点Q从点B出发，以每秒1个单位沿射线BA方向运动，当点P到达点C处时，两点同时停止运动。问当t为何值时，以A、P、Q为顶点的三角形与△OAB相似？
（3）若M为线段AB上一个动点，过点M作MN平行于y轴交抛物线于点N．
①是否存在这样的点M，使得四边形OMNB恰为平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．
②当点M运动到何处时，四边形CBNA的面积最大？求出此时点M的坐标及四边形CBAN面积的最大值．
随着“六一”临近，儿童礼品开始热销，某厂每月固定生产甲、乙两种礼品共100万件，甲礼品每件成本15元，乙礼品每件成本12元，现甲礼品每件售价22元，乙礼品每件售价18元，且都能全部售出。
(1)若某月销售收入2000万元，则该月甲、乙礼品的产量分别是多少？
(2)如果每月投入的总成本不超过1380万元，应怎样安排甲、乙礼品的产量，可使所获得的利润最大？
(3)该厂在销售中发现：甲礼品售价每提高1元，销量会减少4万件，乙礼品售价不变，不管多少产量都能卖出。在（2）的条件下，为了获得更大的利润，该厂决定提高甲礼品的售价，并重新调整甲、乙礼品的生产数量，问：提高甲礼品的售价多少元时可获得最大利润，最大利润为多少万元？
某市规划局计划在一坡角为16°的斜坡AB上安装一球形雕塑，其横截面示意图如图所示.已知支架AC与斜坡AB的夹角为28°，支架BD⊥AB于点B，且AC、BD的延长线均过⊙O的圆心，AB=12m，⊙O的半径为1.5m,求雕塑最顶端到水平地面的垂直距离.（结果精确到0.01m）
(参考数据：cos28°≈0.9,sin62°≈ 0.9, sin44°≈0.7, cos46°≈ 0.7)
已知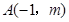
与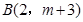
是反比例函数
图象上的两个点。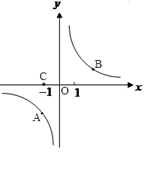
(1)求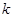
的值；
(2)求直线AB的函数解析式；
(3)若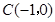点
，点
是反比例函数图象上的一点，如果以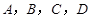
四点为顶点的四边形为梯形，请你求出点的坐标（能求出一个点即可）
|
。
在
ABCD中，E、F分别是AB、CD的中点，连接AF、CE．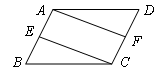
(1)求证：△BEC≌△DFA；
(2)连接AC，当CA＝CB时，判断四边形AECF是什么特殊四边形？并证明你的结论．
为增强环保意识，某社区计划开展一次“减碳环保，减少用车时间”的宣传活动，对部分家庭五月份的平均每天用车时间进行了一次抽样调查，并根据收集的数据绘制了下面两幅不完整的统计图．请根据图中提供的信息，解答下列问题：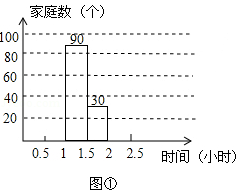
（1）本次抽样调查了多少个家庭？
（2）将图①中的条形图补充完整，直接写出用车时间的中位数落在哪个时间段内；
（3）求用车时间在1～1.5小时的部分对应的扇形圆心角的度数；
（4）若该社区有车家庭有1600个，请你估计该社区用车时间不超过1.5小时的约有多少个家庭？