已知:如图,把矩形OCBA放置于直角坐标系中,OC=3,BC=2,取AB的中点M,连结MC,把△MBC沿x轴的负方向平移OC的长度后得到△DAO。
(1)直接写出点D的坐标;
(2)已知点B与点D在经过原点的抛物线上,点P在第一象限内的该抛物线上移动,过点P作PQ⊥x轴于点Q,连结OP。若以O、P、Q为顶点的三角形与△DAO相似,试求出点P的坐标。
如图,已知AB=AE,∠B=∠E,BC=ED,F是CD中点,求证:AF⊥CD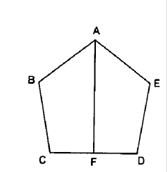
在△ABC中,AB=AC,∠BAC=α,点D是BC上一动点(不与B、C重合),将线段AD绕点A逆时针旋转α后到达AE位置,连接DE、CE,设∠BCE=β.
(1)如图1,若α=90°,求β的大小;
(2)如图2,当点D在线段BC上运动时,试探究α与β之间的数量关系,并证明你的结论;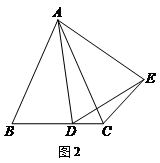
(3)当点D在线段BC的反向延长线上运动时(画出图形),(2)中的结论是否仍然成立?若成立,请证明,若不成立,请直接写出α与β之间的数量关系.
如图,在Rt△ABC中,AB=AC,∠BAC=90,O为BC的中点。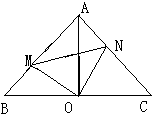
(1)写出点O到△ABC的三个顶点A、B、C的距离的关系(不要求证明)
(2)如果点M、N分别在线段AB、AC上移动,在移动过程中保持AN=BM,请判断△OMN的形状,请证明你的结论。
阅读下面的材料: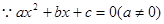 的根为
的根为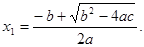 ,
,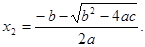
∴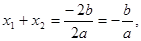
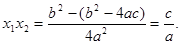
综上所述得,设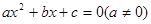 的两根为
的两根为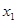 、
、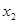 ,则有
,则有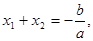

请利用这一结论解决下列问题:
设方程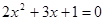 的根为
的根为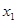 、
、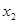 ,求x
,求x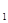
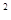 +x
+x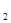
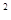 的值。
的值。
如图,在等边△ABC中,已知点D、E分别在BC、AB上,且BD=AE,AD与CE交于点F。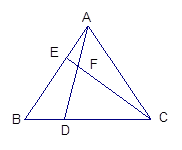
(1)求证:AD=CE
(2)求∠DFC的度数。