设二次函数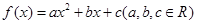 满足下列条件:
满足下列条件:
①当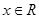 时,
时, 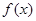 的最小值为0,且
的最小值为0,且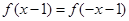 恒成立;
恒成立;
②当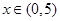 时,
时,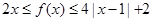 恒成立.
恒成立.
(I)求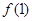 的值;
的值;
(Ⅱ)求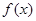 的解析式;
的解析式;
(Ⅲ)求最大的实数m(m>1),使得存在实数t,只要当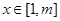 时,就有
时,就有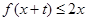 成立
成立
已知定义在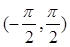 的函数
的函数
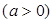 ,在
,在 处的切线斜率为
处的切线斜率为
(Ⅰ)求 及
及 的单调区间;
的单调区间;
(Ⅱ)当 时,
时, 恒成立,求
恒成立,求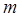 的取值范围.
的取值范围.
设 为抛物线
为抛物线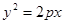 (
(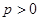 )的焦点,
)的焦点, 为该抛物线上三点,若
为该抛物线上三点,若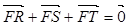 ,且
,且
(Ⅰ)求抛物线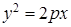 的方程;
的方程;
(Ⅱ)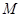 点的坐标为(
点的坐标为(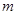 ,
, )其中
)其中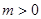 ,过点F作斜率为
,过点F作斜率为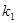 的直线与抛物线交于
的直线与抛物线交于 、
、 两点,
两点, 、
、 两点的横坐标均不为
两点的横坐标均不为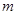 ,连结
,连结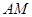 、
、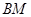 并延长交抛物线于
并延长交抛物线于 、
、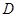 两点,设直线
两点,设直线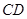 的斜率为
的斜率为 .若
.若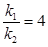 ,求
,求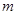 的值.
的值.
如图,在四棱锥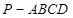 中,
中, ⊥底面
⊥底面 ,四边形
,四边形 是直角梯形,
是直角梯形, ⊥
⊥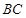 ,
, ∥
∥ ,
,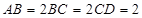 .
.
(Ⅰ)求证:平面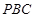 ⊥平面
⊥平面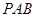 ;
;
(Ⅱ)若二面角 的余弦值为
的余弦值为 ,求
,求 .
.
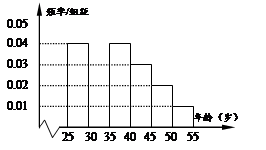
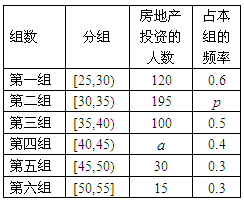
某班同学在“十八大”期间进行社会实践活动,对[25,55]岁的人群随机抽取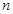 人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
人进行了一次当前投资生活方式----“房地产投资”的调查,得到如下统计和各年龄段人数频率分布直方图:
(Ⅰ)求n,a,p的值;
(Ⅱ)从年龄在[40,50)岁的“房地产投资”人群中采取分层抽样法抽取9人参加投资管理学习活动,其中选取3人作为代表发言,记选取的3名代表中年龄在[40,45)岁的人数为 ,求
,求 的分布列和期望
的分布列和期望 .
.
设等比数列{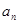 }的前
}的前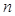 项和为
项和为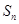 ,已知对任意的
,已知对任意的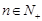 ,点
,点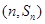 ,均在函数
,均在函数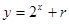 的图像上.
的图像上.
(Ⅰ)求 的值;
的值;
(Ⅱ)记 求数列
求数列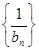 的前
的前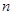 项和
项和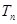 .
.