设数列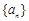 是有穷等差数列,给出下面数表:
是有穷等差数列,给出下面数表: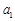

 ……
…… 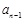
 第1行
第1行
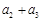 ……
……  第2行
第2行
… … …
… …
… 第n行
上表共有行,其中第1行的个数为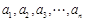 ,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为
,从第二行起,每行中的每一个数都等于它肩上两数之和.记表中各行的数的平均数(按自上而下的顺序)分别为 .
.
(1)求证:数列 成等比数列;
成等比数列;
(2)若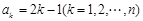 ,求和
,求和 .
.
、(本小题满分16分)
已知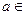 R,函数
R,函数
 R,
R, 为自然对数的底数)。
为自然对数的底数)。
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)若函数 在
在 上单调递增,求
上单调递增,求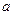 的取值范围;
的取值范围;
(3)函数 是否为R上的单调函数,若是,求出
是否为R上的单调函数,若是,求出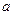 的取值范围;若不是,请说明理由。
的取值范围;若不是,请说明理由。
、(本小题满分14分)
设函数 ,其中实常数
,其中实常数 。
。
(1)求函数 的定义域和值域;
的定义域和值域;
(2)试探究函数 的奇偶性与单调性,并证明你的结论。
的奇偶性与单调性,并证明你的结论。
、(本小 题满分14分)
题满分14分)
已知函数
(1)画出函数在 的简图;
的简图;
(2)写出函数的最小正周期和单调递增区间;并求:当x为何值时,函数有最大值?最大值是多少?
(3)若x是△ABC的一个内角,且y2=1,试判断△ABC的形状。
、(本小题满分14分)
在平面直角坐标系xoy中,点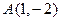 、
、 、
、 。
。
(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足 ,求t的值。
,求t的值。
(本小题满分14分)
已知m>0,设命题 函数
函数 在
在 上单调递减;命题
上单调递减;命题 关于x的不等式
关于x的不等式 的解集为R。若命题
的解集为R。若命题 与
与 有且仅有一个正确,求
有且仅有一个正确,求 的取值范围。
的取值范围。