完成下面的证明：已知，如图，AB∥CD，EG平分∠BEF，FG平分∠EFD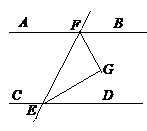
求证：∠EGF＝90°
证明：∵HG∥AB(已知) ∴∠1＝∠3( )
又∵HG∥CD(已知) ∴∠2＝∠4( )
∵AB∥CD(已知) ∴∠BEF＋___________＝180°( )
又∵EG平分∠BEF(已知) ∴∠1＝
∠______( )
又∵FG平分∠EFD(已知) ∴∠2＝∠ ( )
∴∠1＋∠2＝(___________＋______________) ∴∠1＋∠2＝90°
∴∠3＋∠4＝90°( )即∠EGF＝90°
如图，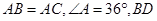
是∠ABC的角平分线，求证：
∽
．
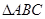如图（1），Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D。AF平分∠CAB，交CD于点E，交CB于点F。
（1）求证：CE=CF。
（2）将图（1）中的△ADE沿AB向右平移到△A′D′E′的位置，使点E′落在BC边上，其它条件不变，如图(2)所示。试猜想：BE′与CF有怎样的数量关系？请证明你的结论。
某校为了丰富学生的校园生活，准备购进一批篮球和足球，其中篮球的单价比足球的单价多40元，用1500元购进的篮球个数与900元购进的足球个数相同，篮球与足球的单价各是多少元？
如图，在平面直角坐标系xoy中，A(-1，5)，B(-1，0)，C(-4，3)。
（1）求出△ABC的面积；
（2）在图中作出△ABC关于y轴的对称图形△A1B1C1；
（3）写出点A1，B1，C1的坐标。
先化简，再求值：(x+1+
)÷
，其中
．