(本小题12分)已知f(x)= 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数.
(Ⅰ)求实数a的值组成的集合A;
(Ⅱ)设关于x的方程f(x)= 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
海中有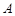 岛,已知
岛,已知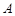 岛四周
岛四周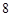 海里内有暗礁,现一货轮由西向东航行,在
海里内有暗礁,现一货轮由西向东航行,在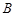 处望见
处望见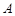 岛在北偏东
岛在北偏东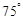 ,再航行
,再航行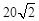 海里到
海里到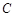 后,见
后,见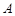 岛在北偏东
岛在北偏东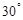 ,如货轮不改变航向继续航行,有无触礁的危险?(
,如货轮不改变航向继续航行,有无触礁的危险?(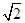 ≈1.4,
≈1.4,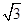 ≈1.7,
≈1.7,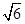 ≈2.4)
≈2.4)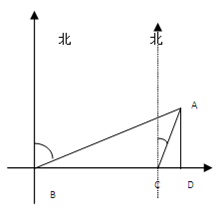
△ABC中D是BC上的点,AD平分 BAC,BD=2DC.
BAC,BD=2DC.
(1)求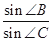 ;
;
(2)若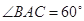 ,求
,求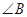 .
.
(本小题满分12分)已知函数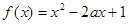 在区间
在区间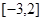 上有最小值,记作
上有最小值,记作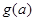
(Ⅰ)求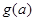 的函数表达式;
的函数表达式;
(Ⅱ)求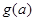 的最大值.
的最大值.
(本小题满分12分)函数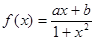 是定义在
是定义在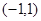 上的奇函数,且
上的奇函数,且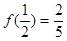 .
.
(Ⅰ)确定函数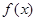 的解析式;
的解析式;
(Ⅱ)用定义证明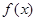 在
在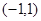 上是增函数;
上是增函数;
(本小题满分12分)已知二次函数 满足
满足 且方程
且方程 有等根.
有等根.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)求 的值域;
的值域;
(Ⅲ)是否存在实数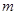 、
、 ,使
,使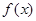 的定义域为
的定义域为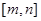 、值域为
、值域为 .若存在,求出
.若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.