不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为 .
.
(1)求袋中蓝球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法,求两次摸到都是白球的概率.
如图,在 中,
中, ,
, ,
, ,动点
,动点 (与点
(与点 不重合)在
不重合)在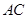 边上,
边上, 交
交 于
于 点.
点.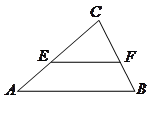
(1)当 的面积与四边形
的面积与四边形 的面积相等时,求
的面积相等时,求 的长;
的长;
(2)当 的周长与四边形
的周长与四边形 的周长相等时,求
的周长相等时,求 的长;
的长;
(3)试问在 上是否存在点
上是否存在点 ,使得
,使得 为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出
为等腰直角三角形?若不存在,请简要说明理由;若存在,请求出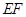 的长.
的长.
如图, 、
、 是反比例函数
是反比例函数 (k>0)在第一象限图象上的两点,点
(k>0)在第一象限图象上的两点,点 的坐标为(2,0),若△
的坐标为(2,0),若△ 与△
与△ 均为等边三角形.
均为等边三角形.
(1)求此反比例函数的解析式;
(2)求 点的坐标.
点的坐标.
某商场礼品柜台春节期间购进大量贺年卡,一种贺年卡平均每天可售出500张,每张盈利0.3元.为了尽快减少库存,商场决定采取适当的降价措施,调查发现,如果这种贺年卡的售价每降低0.1元,那么商场平均每天可多售出100张,商场要想平均每天盈利120元,每张贺年卡应降价多少元?
(10分)10分)已知 ,
, 是一次函数
是一次函数 的图象和反比例函数
的图象和反比例函数 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线 与
与 轴的交点
轴的交点 的坐标及△
的坐标及△ 的面积;
的面积;
(3)求不等式 的解集(请直接写出答案).
的解集(请直接写出答案).
(10分)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD,等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.