(1)小张自主创业开了一家服装店,因为进货时没有进行市场调查,在换季时积压了一批服装。为了缓解资金压力,小张决定打折销售。若每件服装按标价的5折出售将亏20元,而按标价的8折出售将赚40元。
①请你算一算每件服装的标价是多少元?
②为了尽快减少库存,又要保证不亏本,请你告诉小张最多能打几折。
(2)小张认真总结了前一次的教训,进行了详细的市场调查后第二次进货500件,按第一次的标价销售了300件后,剩下的进行甩卖,为了尽快减少库存,又要保证盈利两万元钱,请你告诉小张最多能打几折。
用配方法解方程:
如图,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系.已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.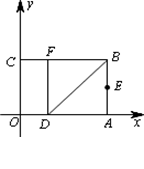
(1)直接写出点E、F的坐标;
(2)设顶点为F的抛物线交y轴正半轴于点P,且以点E、F、P为顶点的三角形是等腰三角形,求该抛物线的解析式;
(3)在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.
已知:如图,抛物线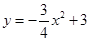 与
与 轴交于点
轴交于点 ,点
,点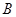 ,与直线
,与直线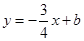 相交于点
相交于点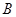 ,点
,点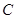 ,直线
,直线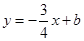 与
与 轴交于点
轴交于点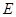 .
.
(1)求
 的面积.
的面积.(2)若点
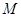 在线段
在线段 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从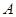 向
向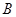 运动(不与
运动(不与 重合),同时,点
重合),同时,点 在射线
在射线 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从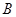 向
向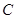 运动.设运动时间为
运动.设运动时间为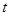 秒,请写出
秒,请写出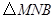 的面积
的面积 与
与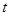 的函数关系式,并求出点
的函数关系式,并求出点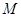 运动多少时间时,
运动多少时间时,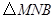 的面积最大,最大面积是多少?
的面积最大,最大面积是多少?
已知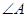 是
是 的一个内角,抛物线
的一个内角,抛物线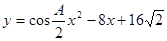 的顶点在
的顶点在 轴上.
轴上.(1)求
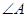 的度数;
的度数;(2) 若
 求:AB边的长.
求:AB边的长.
如图(1),由直角三角形边角关系,可将三角形面积公式变形,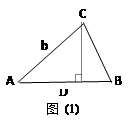
即: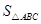 =
=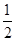 AB·CD,
AB·CD,
在Rt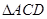 中,
中,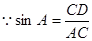 ,
,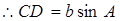
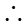
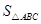 =
=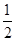 bc·sin∠A.①
bc·sin∠A.①
即三角形的面积等于两边之长与夹角正弦之积的一半.
如图(2),在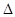 ABC中,CD⊥AB于D,∠ACD=α,∠DCB=β.
ABC中,CD⊥AB于D,∠ACD=α,∠DCB=β.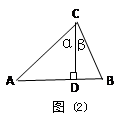
∵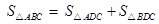 ,由公式①,得
,由公式①,得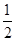 AC·BC·sin(α+β)=
AC·BC·sin(α+β)= 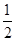 AC·CD·sinα+
AC·CD·sinα+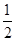 BC·CD·sinβ,
BC·CD·sinβ,
即 AC·BC·sin(α+β)= AC·CD·sinα+BC·CD·sinβ.②
请你利用直角三角形边角关系,消去②中的AC、BC、CD,只用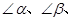
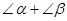 的正弦或余弦函数表示(直接写出结果).
的正弦或余弦函数表示(直接写出结果).(1)______________________________________________________________
(2)利用这个结果计算:
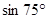 =_________________________
=_________________________