如图所示，一固定粗糙斜面与水平面夹角
。一个质量
的小物体（可视为质点），在F＝10 N的沿斜面向上的拉力作用下，由静止开始沿斜面向上运动。已知斜面与物体间的动摩擦因数
，取
。试求：
（1）物体在拉力F作用下运动的加速度
；
（2）若力F作用1.2 s后撤去，物体在上滑过程中距出发点的最大距离s；
（3）物体从静止出发，到再次回到出发点的过程中，物体克服摩擦所做的功
。
交流发电机矩形线圈边长ab="cd=0.4" m，bc="ad=0.2" m，共50匝，线圈电阻r="1" Ω，线圈在B="0.2" T的匀强磁场中，绕垂直磁场方向的轴OO′以200 rad/s的角速度匀速转动，外接电阻R=7Ω，如图所示。求：
（1）从图示位置开始计时，线圈中产生的感应电动势大小随时间变化的函数表达式；
（2）电压表读数；
（3）电阻R上的电功率。
(9分)如图所示，水平放置的导体框架，宽L＝0.5 m，接有电阻R＝0.3Ω，整个装置处于垂直框架平面向下的匀强磁场中，磁感应强度B＝0.4 T．一导体棒ab垂直框边跨放在框架上，并能无摩擦地在框架上滑动，已知导体棒ab的电阻为
，框架的电阻均不计．当ab以v＝5.0 m/s的速度向右匀速滑动时，求：
（1）ab棒中产生的感应电流的大小和方向；
（2）维持导体棒ab做匀速运动的外力F的大小。
如图所示的电路中，R2=30Ω，R3=15Ω， S闭合时，电压表V的示数为11.4V，电流表A的示数为0.2A，S断开时，电流表A的示数为0.3A，求：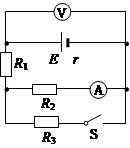
（1）电阻R1的值；
（2）电源电动势E和内阻r的值。
如图所示，在第一象限有一匀强电场，场强大小为E，方向与y轴平行；一质量为m、电荷量为－q(q>0)的粒子以平行于x轴的速度从y轴上P点处射入电场，已知OP＝L，OQ＝2
L.不计粒子重力．求：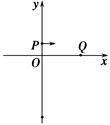
(1)粒子在第一象限中运动的时间．
(2)粒子离开第一象限时速度方向与x轴的夹角．
将一个电量为1×10－6C的负电荷从电场中的A点移到B点，克服电场力做功2×10－6J。从C点移到D点，电场力做功7×10－6J。若已知B点电势比C点高3V，求（1）A到B的电势差；（2）A到D的电势差；（3）设C点的电势为零，则D点的电势为多少？