(1)先化简,再求值 ,其中
,其中 满足
满足 ;
;
(2)已知多项式 ,其中
,其中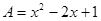 ,小马在计算
,小马在计算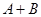 时,由于粗心把
时,由于粗心把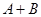 看成了
看成了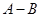 求得结果为
求得结果为 ,请你帮小马算出
,请你帮小马算出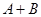 的正确结果。
的正确结果。
如图所示,AB//CD,∠ACD= .
.
⑴用直尺和圆规作∠C的平分线CE,交AB于E,并在CD
上取一点F,使AC=AF,再连接AF,交CE于K;
(要求保留作图痕迹,不必写出作法)
⑵依据现有条件,直接写出图中所有相似的三角形﹒
(图中不再增加字母和线段,不要求证明)
如图所示,一次函数 与反比例函数
与反比例函数 的图象相交于A,B两点,且与坐标轴的交点为
的图象相交于A,B两点,且与坐标轴的交点为 ,
, ,点B的横坐标为
,点B的横坐标为 .
.
(1)试确定反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出不等式 的解.
的解.
如图所示,在平行四边形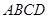 的各边
的各边 上,分别取点
上,分别取点 ,使
,使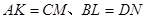 .
.
求证:四边形 为平行四边形.
为平行四边形.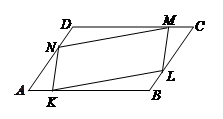
解不等式组:
(本题共2小题,第(1)小题5分,第(2)小题6分,共11分)
|
(1)计算:  +
+
 (
( )
) -
-  ;
;