甲、乙等五名奥运志愿者被随机地分到 四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加
四个不同的岗位服务,每个岗位至少有一名志愿者.(Ⅰ)求甲、乙两人同时参加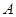 岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量
岗位服务的概率;(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;(Ⅲ)设随机变量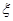 为这五名志愿者中参加
为这五名志愿者中参加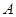 岗位服务的人数,
岗位服务的人数, 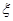 可取何值?请求出相应的
可取何值?请求出相应的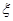 值的分布列.
值的分布列.
(本小题满分14分)
设函数 是定义域在R上的奇函数.
是定义域在R上的奇函数.
(1)若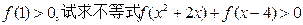 的解集;
的解集;
(2)若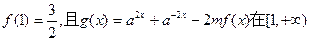 上的最小值为—2,求m的值.
上的最小值为—2,求m的值.
(本小题 满分13分)某公司是专门生产健身产品的企业,第一批产品
满分13分)某公司是专门生产健身产品的企业,第一批产品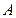 上市销售40天内全部售完,该公司对第一批产品
上市销售40天内全部售完,该公司对第一批产品 上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品
上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品 的销售利润与上市时间的关系.
的销售利润与上市时间的关系.
(1)写出市场的日销售量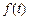 与第一批产品A上市时间t的关系式;
与第一批产品A上市时间t的关系式;
(2)第一批产品A上市后的第几天,这家公司日销售利润最大,最大利润是多少?
(本小题满分12分)
已知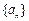 是一个公差大于
是一个公差大于 的等差数列,且满足
的等差数列,且满足 ,
, 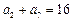 .
.
(1) 求数列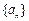 的通项公式;
的通项公式;
(2) 若数列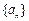 和数列
和数列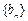 满足等式:
满足等式: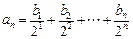 (
( 为正整数), 求数列
为正整数), 求数列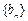 的前
的前 项和
项和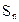 .
.
(本小题满分12分)
已知函数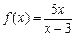 ,
,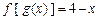 .(1)求
.(1)求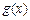 的解析式;(2) 求
的解析式;(2) 求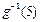 的值.
的值.
已知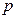 :
: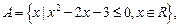
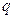 :
: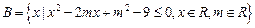 .
.
(1)若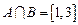 ,求实数
,求实数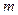 的值;
的值;
( 2)若
2)若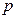 是
是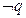 的充分条件,求实数
的充分条件,求实数 的取值范围.
的取值范围.