如图所示,足够长的光滑平行金属导轨MN、PQ固定在一个水平面上,两导轨间距L=0.2m,在两导轨左端M、P间连接阻值R=0.4 的电阻,导轨上停放一质量为m=0.1
的电阻,导轨上停放一质量为m=0.1 ,电阻r=0.1
,电阻r=0.1 的金属杆CD,导轨阻值可忽略不计,整个装置处于方向竖直方向上,磁感应强度大小B=0.5T的匀强磁场中,现用一大小为0.5N的恒力F垂直金属杆CD沿水平方向拉杆,使之由静止开始向右运动,金属杆向右运动位移x=1m后速度恰好达到最大,求:
的金属杆CD,导轨阻值可忽略不计,整个装置处于方向竖直方向上,磁感应强度大小B=0.5T的匀强磁场中,现用一大小为0.5N的恒力F垂直金属杆CD沿水平方向拉杆,使之由静止开始向右运动,金属杆向右运动位移x=1m后速度恰好达到最大,求:
(1)整个运动过程中拉力F的最大功率;
(2)从开始运动到金属杆的速度达到最大的这段时间内通过电阻R的电量。
一辆值勤的警车停在公路边,当警员发现从他旁边以10 m/s的速度匀速行驶的货车有违章行为时,决定前去追赶,经过5.5 s后警车发动起来,并以2.5 m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在90 km/h以内。问:
(1)警车在追赶货车的过程中,两车间的最大距离是多少?
(2)警车发动后要多长时间才能追上货车?
在竖直的井底,将一物块以11 m/s的速度竖直向上抛出,物块经过井口时被人接住,在被人接住前1 s内物块的位移是4 m,位移方向向上,不计空气阻力,g取10 m/s2,求:
(1)物块从抛出到被人接住所经历的时间;
(2)此竖直井的深度。
一同学想设计一个轨道玩具,其设想是将一光滑的倾角为θ斜面轨道和一半径为r的光滑半圆弧轨道两轨道平滑无缝连接,半圆弧轨道最高点和最低点在同一竖直线上,在轨道连接处无能量损失,让一小球从斜面上某一位置由静止释放,沿斜面轨道和半圆弧轨道运动,经过圆弧的顶点水平抛出并垂直落在斜面上,如图所示,如果他的想法可行,则斜面倾角θ应满足什么条件?在满足条件的情况下,小球释放位置距斜面底端高h为? 
如图所示,在倾角为37o的斜面上,一劲度系数为k=100N/m的轻弹簧一端固定在A点,自然状态时另一端位于B点。斜面上方有一半径R=0.2m、圆心角等于143°的竖直圆弧形光滑轨道与斜面相切于C处,圆弧轨道的最高点为D。斜面AB段光滑,BC段粗糙且长度为0.4m。现将一质量为1kg的小物块从C点由静止释放,小物块将弹簧压缩了0.2m后速度减为零(不计小物块到达B处与弹簧碰撞时的能量损失)。已知弹簧弹性势能表达式Ek=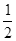 kx2,其中k为弹簧的劲度系数,x为弹簧的形变量,重力加速度取g=10m/s2,sin37o=0.6,cos37o=0.8。(计算结果可保留根号)求:
kx2,其中k为弹簧的劲度系数,x为弹簧的形变量,重力加速度取g=10m/s2,sin37o=0.6,cos37o=0.8。(计算结果可保留根号)求: 
⑴小物块与斜面BC段间的动摩擦因数μ
⑵小物块第一次返回BC面上时,冲到最远点E,求BE长
⑶若用小物块将弹簧压缩,然后释放,要使小物块在CD段圆弧轨道上运动且不脱离圆弧轨道,则压缩时压缩量应满足的条件
土星上空有许多大小不等的岩石颗粒,其绕土星的运动可视为圆周运动。其中有两个岩石颗粒A和B与土星中心距离分别为rA=8.0×104 km和rB=1.2×105 km。忽略所有岩石颗粒间的相互作用。(结果可用根式表示)
⑴求岩石颗粒A和B的线速度之比;
⑵求岩石颗粒A和B的周期之比;
⑶土星探测器上有一物体,在地球上重为10 N,推算出他在距土星中心3.2×105 km处受到土星的引力为0.38 N。已知地球半径为6.4×103 km,请估算土星质量是地球质量的多少倍?