某大学体育学院在2012年新招的大一学生中,随机抽取了 40名男生,他们的身高(单位:cm)情况共分成五组:第1组[175,180),第 2 组[180,185),第 3 组 [185,190),第 4 组[190,195),第 5 组[195,200) .得到的频率分布直方图(局部)如图所示,同时规定身高在185cm以上(含185cm)的学生成为组建该校篮球队的“预备生”.
(I)求第四组的频率并补布直方图;
(II)如果用分层抽样的方法从“预备生”和“非预备生”中选出5人,再从这5人中随机选2人,那么至少有1人是“预备生”的概率是多少?
(III)若该校决定在第4,5组中随机抽取2名学生接受技能测试,第5组中有ζ名学生接受测试,试求ζ的分布列和数学期望.
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比.已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
(1)分别写出两种产品的收益与投资额的函数关系;
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?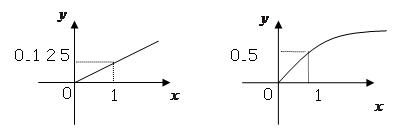
已知函数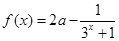 (
(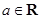 ).
).
(1)若函数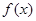 为奇函数,求
为奇函数,求 的值;
的值;
(2)判断函数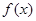 在
在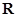 上的单调性,并证明.
上的单调性,并证明.
已知函数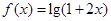 ,
, .
.
(1)求函数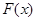 的定义域;
的定义域;
(2)当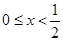 时,总有
时,总有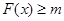 成立,求
成立,求 的取值范围.
的取值范围.
已知函数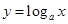 在
在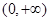 上是减函数,求函数
上是减函数,求函数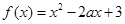 在
在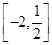 上的最大值与最小值.
上的最大值与最小值.
已知函数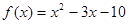 的两个零点为
的两个零点为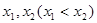 ,
,
设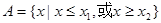 ,
,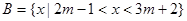 ,且
,且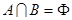 ,求实数
,求实数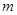 的取值范围.
的取值范围.