在古腊毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形
则第 个三角形数为 ( )
个三角形数为 ( )
A. |
B.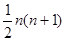 |
C. |
D. |
定义 ,设
,设 的取值范围是()
的取值范围是()
| A.[-7,10] | B.[—6,10] | C.[-6,8] | D.[—7,8] |
在棱长为1的正方形ABCD—A1B1C1D1的底面A1B1C1D1内取一点E,使AE与AB、AD所成的角都是60°,则线段AE的长为()
A. B.
B.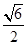 C.
C. D.
D.
已知a,b,c分别为△ABC的三个内角A,B,C的对边,向量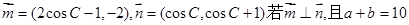 ,则△ABC周长的最小值为()
,则△ABC周长的最小值为()
A.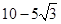 |
B.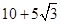 |
C.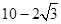 |
D. |
如图,正六边形ABCDEF的两个项点,A、D为双曲线的两个焦点,其余4个顶点都在双曲线上,则该双曲线的离心率是()
A.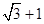 B.
B.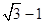
C.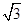 D.
D.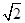
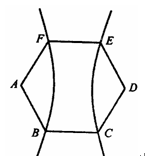
如图,设D是图中所示的矩形区域,E是D内函数 图象上方的点构成的区域。向D中随机投
图象上方的点构成的区域。向D中随机投
一点,则该点落入E(阴影部分)中的概率为()
A. |
B. |
C. |
D. |