已知双曲线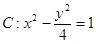 ,
,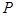 为
为 上任意一点;
上任意一点;
(1)求证:点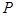 到双曲线
到双曲线 的两条渐近线的距离的乘积是一个常数;
的两条渐近线的距离的乘积是一个常数;
(2)设点 ,求
,求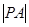 的最小值.
的最小值.
数列
满足
,
,
是常数。
(Ⅰ)当
时,求
及
的值;
(Ⅱ)数列
是否可能为等差数列?若可能,求出它的通项公式;若不可能,说明理由;
(Ⅲ)求
的取值范围,使得存在正整数
,当
时总有
。
已知
的顶点
在椭圆
上,
在直线
上,且
.
(Ⅰ)当
边通过坐标原点
时,求
的长及
的面积;
(Ⅱ)当
,且斜边
的长最大时,求
所在直线的方程。
甲、乙等五名奥运志愿者被随机地分到
四个不同的岗位服务,每个岗位至少有一名志愿者。
(Ⅰ)求甲、乙两人同时参加
岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率。
已知函数
,且
是奇函数.
(Ⅰ)求
的值;
(Ⅱ)求函数
的单调区间.
如图,在三棱锥 中, , , , .
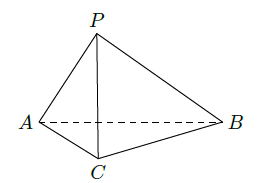
(Ⅰ)求证:
;
(Ⅱ)求二面角
的大小.