解不等式 >0
>0
(本小题满分12分)一种电子玩具按下按钮后,会出现红球或绿球.已知按钮第一次按下后,出现红球与绿球的概率都是 从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为
从按钮第二次按下起,若前次出现红球,则下一次出现红球、绿球的概率分别为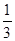 、
、 ;若前次出现绿球,则下一次出现红球,绿球的概率分别为
;若前次出现绿球,则下一次出现红球,绿球的概率分别为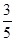 、
、
记第 次按下按钮后出现红的概率为Pn.
次按下按钮后出现红的概率为Pn.
(1)求P2的值;
(2)当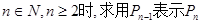 的表达式;
的表达式;
(3)求Pn关于n的表达式.
(本小题满分12分)万州区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
(Ⅰ)求y关于t的线性回归方程;
(Ⅱ)利用(Ⅰ)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ,
,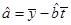
(本小题满分13分)从万州二中高二年级文科学生中随机抽取60名学生,将其月考的政治成绩(均为整数)分成六段:  ,
,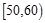 ,…,
,…,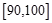 后得到如下频率分布直方图 .
后得到如下频率分布直方图 .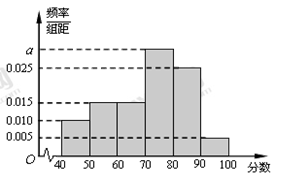
(Ⅰ)求分数在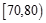 内的频率;
内的频率;
(Ⅱ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样 本看成一个总体,从中任意选取2人, 求其中恰有1人的分数不低于90分的概率.
(本小题满分13分)2008年5月12日14时28分04秒,四川省阿坝藏族羌族自治州汶川县发生里氏8.0级地震,地震造成69227人遇难,374643人受伤,17923人失踪。重庆众多医务工作者和志愿者加入了抗灾救援行动。其中重庆三峡中心医院外科派出由5名骨干医生组成的救援小组,奔赴受灾第一线参与救援。现将这5名医生分别随机分配到受灾最严重的汶川县、北川县、绵竹三县中的某一个。
(1)求每个县至少分配到一名医生的概率。
(2)若将随机分配到汶川县的人数记为 ,求随机变量
,求随机变量 的分布列,期望和方差。
的分布列,期望和方差。
(本小题满分13分) 已知二项式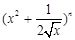 (
( N*)展开式中,前三项的二项式系数和是
N*)展开式中,前三项的二项式系数和是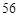 ,求:(Ⅰ)求
,求:(Ⅰ)求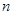 的值;
的值;
(Ⅱ)展开式中的常数项.