如图所示,点A,F,C,D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.
(1)求证:四边形BCEF是平行四边形;
(2)若∠ABC=90°,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形.
如图,⊙A、⊙B、⊙C两两不相交,且半径都是2cm,图中的三个扇形(即三个阴影部分)的面积之和是多少?弧长的和为多少?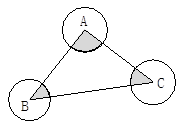
先阅读,再解答:
我们在判断点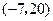 是否在直线
是否在直线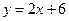 上时,常用的方法:把
上时,常用的方法:把 代入
代入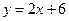 中,由
中,由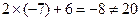 ,判断出点
,判断出点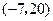 不在直线
不在直线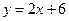 上。小明由此方法并根据“两点确定一条直线”,推断出点A(1,2),B(3,4),C(-1,6)三点可以确定一个圆。你认为他的推断正确吗?请你利用上述方法说明理由。
上。小明由此方法并根据“两点确定一条直线”,推断出点A(1,2),B(3,4),C(-1,6)三点可以确定一个圆。你认为他的推断正确吗?请你利用上述方法说明理由。
解方程: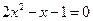 。
。
在如图所示的2004年1月份日历中,
| 星期日 |
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
| 1 |
2 |
3 |
||||
| 4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 11 |
12 |
13 |
14 |
15 |
16 |
17 |
| 18 |
19 |
20 |
21 |
22 |
23 |
24 |
| 25 |
26 |
27 |
28 |
29 |
30 |
31 |
用一个长方形的方框圈出任意3×3个数.如果从左下角到右上角的“对角线”上的3个数字的和为45,那么这9个数的和为,在这9个日期中,最后一天是号;
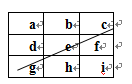
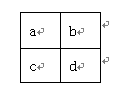
用一个长方形方框圈出任意2×2个数(如4,5,11,12),你能发现这四个数有怎样的关系?请用一个等式表示a,b,c,d 之间的关系.
某一中学位于东西方向的一条路上,一天我们学校的李老师出校门去家访,他先向东走100米到聪聪家,再向西走150米到青青家,再向东走200米到刚刚家,请问: 聪聪家与刚刚家相距多远?
如果把这条路看作一条数轴,以向东为正方向,以校门口为原点,请你在这条数轴上标出他们家与学校的大概位置(数轴上50米表示单位1).
聪聪家向西210米所表示的数是多少?
你认为可用什么办法求数轴上两点之间的距离?