如图所示,已知m、n是方程 的两个实数根,且m<n,抛物线
的两个实数根,且m<n,抛物线 的图像经过点A(m,0)、B(0,n).
的图像经过点A(m,0)、B(0,n). 
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的顶点为D,试求出点C、D的坐标和△BCD的面积;
(注:抛物线 的顶点坐标为
的顶点坐标为
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛物线交于H点,若直线BC把△PCH分成面积之比
为2:3的两部分,请求出P点的坐标.
比较下列各组数的大小:
(1)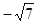 与
与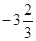 ;(2)
;(2)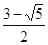 与
与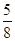 .
.
若△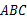 三边满足下列条件,判断△
三边满足下列条件,判断△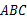 是不是直角三角形,并说明哪个角是直角:
是不是直角三角形,并说明哪个角是直角:
(1)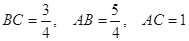 ;
;
(2)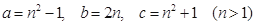 .
.
某餐厅中,一张桌子可坐6人,有以下两种摆放方式: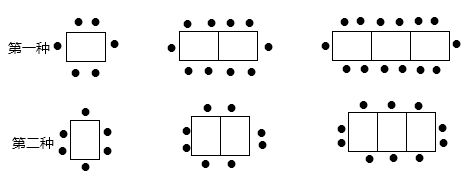
(1)当有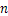 张桌子时,两种摆放方式各能坐多少人?
张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?
某工厂第一车间有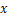 人,第二车间比第一车间人数的
人,第二车间比第一车间人数的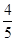 少
少 人,如果从第二车间调出
人,如果从第二车间调出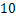 人到第一车间,那么:
人到第一车间,那么:
(1)两个车间共有多少人?
(2)调动后,第一车间的人数比第二车间多多少人?
有这样一道题:
先化简,再计算: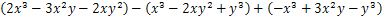 ,
,
其中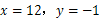 .
.
甲同学把“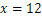 ”错抄成“
”错抄成“ ”,但他计算的结果也是正确的,试说明理由,并求出这个结果.
”,但他计算的结果也是正确的,试说明理由,并求出这个结果.