已知直线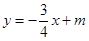
与
轴，
轴分别交于点A和点B，点B的坐标为（0，6）
（1）求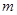
的值和点A的坐标；
（2）在矩形OACB中，某动点P从点B出发以每秒1个单位的速度沿折线B-C-A运动.运动至点A停止.直线PD⊥AB于点D，与轴交于点E.设在矩形OACB中直线PD未扫过的面积为S,运动时间为 t.
①求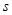
与t的函数关系式；
②⊙Q是△OAB的内切圆，问：t为何值时，PE与⊙Q相交的弦长为2.4 ？
抗震救灾，重建家园. 为了修建在地震中受损的一条公路，若由甲工程队单独修建需3个月完成，每月耗资12万元；若由乙工程队单独修建需6个月完成，每月耗资5万元．
（1）请问甲、乙两工程队合作修建需几个月完成？共耗资多少万元？
（2）若要求最迟4个月完成修建任务．请你设计一种方案，既保证按时完成任务，又最大限度节省资金.（时间按整月计算）
如图，在梯形ABCD中，AD∥BC，AB＝DC，延长CB到E，使BE=AD，连接AE、AC．
（1）求证：AE=AC；
（2）若梯形ABCD的高为2，∠CAD=30°，求梯形ABCD的面积．
暑假期间，某学校同学积极参加社会公益活动.开学后，校团委随机抽取部分学生对每人的“累计参与时间”进行了调查，将数据整理并绘制成如图①、②所示的统计图.请根据这两幅不完整的统计图解答下列问题：
（1）这次调查共抽取了多少名学生？
（2）将图①的内容补充完整；
（3）求图②中“约15小时”对应的圆心角度数，并将图②的内容补充完整．
如图，已知直线
与双曲线
相交于A、B两点，且当x＞1时，y1＞y2；当0＜x＜1时，y1＜y2．
（1）求b的值及A、B两点的坐标；
（2）若在
上有一点C到y轴的距离为3，求△ABC的面积．
如图，在平面直角坐标系xoy中，已知
OABC的两个顶点A、C的坐标分别为（1，2）、（3，0）.
（1）画出OABC关于y轴对称的OA1B1C1，并写出点B1的坐标；
（2）画出OABC绕点O顺时针方向旋转90°后得到的OA2B2C2.