在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.
(·湖北荆门,20题,分)为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如图所示的统计图表.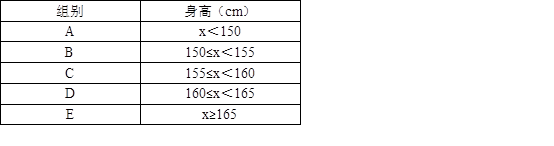
根据图表中信息,回答下列问题:
(1)在样本中,男生身高的中位数落在 组(填组别序号),女生身高在B组的人数有 人;
(2)在样本中,身高在150≤x<155之间的人数共有 人,身高人数最多的在 组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<160之间的学生约有多少人?
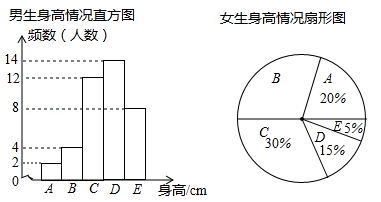
(·湖北黄冈,19题,分)(7 分)“ 六一”儿童节前夕,蕲黄县教育局准备给留守儿童赠送一批学习用品,先对浠泉镇浠泉小学的留守儿童人数进行抽样统计,发现各班留守儿童人数分别为6 名,7 名,8 名,10 名,12 名这五种情形,并将统计结果绘制成了如图所示的两幅不完整的统计图.
请根据上述统计图,解答下列问题:
(1)该校有多少个班级?并补全条形统计图;
(2)该校平均每班有多少名留守儿童?留守儿童人数的众数是多少?
(3)若该镇所有小学共有60 个教学班,请根据样本数据,估计该镇小学生中,共有多少名留守儿童.
(·湖北黄冈,18题,分)在某电视台的一档选秀节目中,有三位评委,每位评委在选手完成才艺表演后,出示“ 通过”(用√表示)或“ 淘汰”(用×表示)的评定结果.节目组规定:每位选手至少获得两位评委的“通过”才能晋级.
(1)请用树形图列举出选手A 获得三位评委评定的各种可能的结果;
(2)求选手A 晋级的概率.
(·湖北鄂州,19题,8分)八年级(1)班学生在完成课题学习“体质健康测试中的数据分析”后,利用课外活动时间积极参加体育锻炼,每位同学从篮球、跳绳、立定跳远、长跑、铅球中选一项进行训练,训练后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图.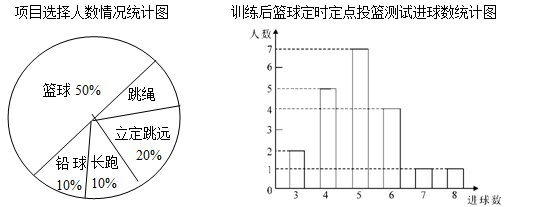
请你根据上面提供的信息回答下列问题:
(1)扇形图中跳绳部分的扇形圆心角为 度,该班共有学生 人,训练后篮球定时定点投篮平均每个人的进球数是 .
(2)老师决定从选择铅球训练的3名男生和1名女生中任选两名学生先进行测试,请用列表或画树形图的方法求恰好选中两名男生的概率.
(·湖北衡阳,24题,分)(本小题满分6分)某校学生会正筹备一个“庆毕业”文艺汇演活动,现准备从4名(其中两男两女)节目主持候选人中,随机选取两人担任节目主持人,请用列表法或画树状图求选出的两名主持人“恰好为一男一女”的概率.