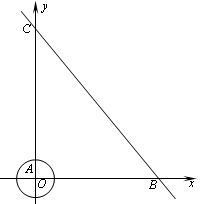
如图,在直角坐标系中,半径为1的⊙A圆心与原点O重合,直线l分别交x轴、y轴于点B、C,若点B的坐标为(6,0),tan∠ABC=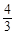 .
.
(1)若点P是⊙A上的动点,求P到直线BC的最小距离,并求此时点P的坐标;
(2)若点A从原点O出发,以1个单位/秒的速度沿着线路OB→BC→CO运动,回到点O停止运动,⊙A随着点A的运动而移动.设点A运动的时间为t.
①求⊙A在整个运动过程中与坐标轴相切时t的取值;
②求⊙A在整个运动过程中所扫过的图形的面积为 .
为了解南宁市的绿化进程,小红同学查询了首府园林绿化政务网,根据网站发布的近几年南宁市城市绿化资源情况的相关数据,绘制了如下统计图(不完整):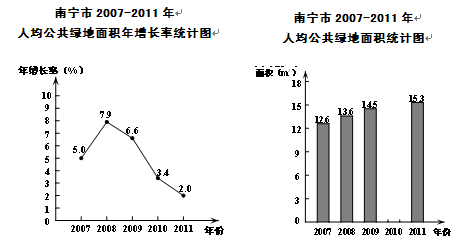
(1)请根据以上信息解答下列问题:
① 2010年南宁市人均公共绿地面积是多少平方米?(精确到0.1)
② 补全条形统计图;
(2)为提高南宁市人均公共绿地面积做贡献. 小红所在学校参加了南宁市植树造林活动,她对所在班级的40名同学2012年参与植树的情况做了调查,并根据调查情况绘制出如下统计表:
| 种树棵数(棵) |
0 |
1 |
2 |
3 |
4 |
5 |
| 人数 |
2 |
1 |
3 |
12 |
13 |
9 |
如果按照小红的统计数据,请你通过计算估计,她所在学校的1500名同学在2012年共植树多少棵.
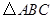 和点
和点 在平面直角坐标系中的位置如图所示:
在平面直角坐标系中的位置如图所示: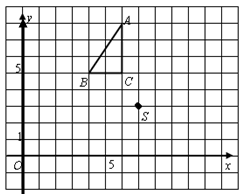
(1)将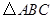 向右平移2个单位得到
向右平移2个单位得到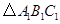 ,则点
,则点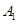 的坐标是,点
的坐标是,点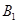 的坐标是 ;
的坐标是 ;
(2)将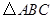 绕点
绕点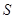 按顺时针方向旋转
按顺时针方向旋转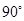 ,画出旋转后的图形.
,画出旋转后的图形.
先化简,再求值.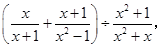 其中
其中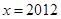
如图,抛物线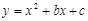 与
与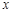 轴交于A(-1,0),B(3,0) 两点.
轴交于A(-1,0),B(3,0) 两点.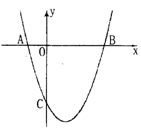
(1) 求该抛物线的解析式;
(2) 设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标;
(3) 设(1)中抛物线交y 轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
如图9-1,9-2,△ABC是等边三角形,D、E分别是AB、BC边上的两个动点(与点A、B、C不重合),始终保持BD=CE.
(1)当点D、E运动到如图9-1所示的位置时,求证:CD=AE.
(2)把图9-1中的△ACE绕着A点顺时针旋转60°到△ABF的位置(如图9-2),分别连结DF、EF.
① 找出图中所有的等边三角形(△ABC除外),并对其中一个给予证明;
② 试判断四边形CDFE的形状,并说明理由