如图1，二次函数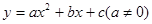
的图象为抛物线，交x轴于A、B两点，交y轴于C点．其中AC=
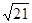，BC=
，
．
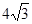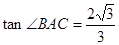（1）求二次函数的解析式；
（2）若P点为抛物线上一动点且在x轴下方运动，当以P为圆心，1为半径的⊙P与直线BC相切时，求出符合条件的P点横坐标；
（3）如图2，若点E从点A出发，以每秒3个单位的速度沿着AB向点B匀速运动，点F从点A出发，以每秒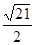
个单位的速度沿着AC向点C匀速运动．两点同时出发，当其中一点到达终点时，另一点也随之停止运动．过点E作AB的垂线
交抛物线于点E′，作点F关于直线的对称点F′．设点E的运动时间为t（s），点F′ 能恰好在抛物线吗？若能，请直接写出t的值；若不能，请说明理由．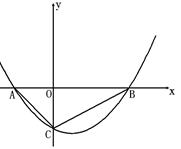
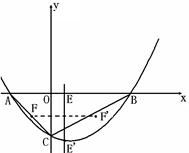
图1 图2
小青在本学期的数学成绩如下表所示（成绩均取整数）：
（1）计算小青本学期的平时平均成绩；
（2）如果学期的总评成绩是根据图所示的权重计算，那么本学期小青的期末考试成绩x至少为多少分才能保证达到总评成绩90分的最低目标？
已知经过闭合电路的电流I与电路的电阻R是反比例函数关系，请根据表格已知条件求出I与R的反比例函数关系式，并填写表格中的空格．
(1) 如图，在等腰梯形ABCD中，AD∥BC，AB∥DE，BC=8，AD=5，求EC的长．
(2)如图是一个外轮廓为矩形的机器零件平面示意图，根据图中的尺寸（单位：mm），计算两圆孔中心
和
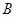的距离．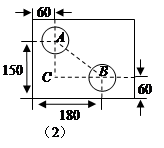
(1) 先化简再求值：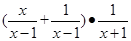
，(2) 解方程：
．
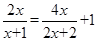其中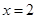
．
(1)一种圆环甲(如图1)，它的外圆直径是8厘米，环宽1厘米。
①如果把这样的2个圆环扣在一起并拉紧(如图2)，长度为厘米；
②如果用n个这样的圆环相扣并拉紧，长度为厘米。
(2)另一种圆环乙，像(1)中圆环甲那样相扣并拉紧，
①3个圆环乙的长度是28cm，5个圆环乙的长度是44cm，求出圆环乙的外圆直径和环宽；
②现有n(n＞2)个圆环甲和n(n＞2)个圆环乙，将它们像(1)中那样相扣并拉紧，长度为多少厘米?