数学兴趣小组测量校园内旗杆的高度，有以下两种方案：
方案一：小明在地面直上立一根标杆EF，沿着直线BF后退到点D，使眼睛C、标杆的顶点E 、旗杆的
顶点A在同一直线上（如图1）．测量：人与标杆的距离DF=1m，人与旗杆的距离DB=16m，人的目高
和标杆的高度差EG=0．9m，人的高度CD=1．6m．
方案二：小聪在某一时刻测得1米长的竹竿竖直放置时影长1．5米，在同时刻测量旗杆的影长时，因
旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙
上的影高为2米（如图2）．
请你结合上述两个方案，分别画出符合题意的示意图，并求出旗杆的高度．
如图①所示，在直角梯形ABCD中，∠BAD=90°，E是直线AB上一点，过E作直线//BC，交直线CD于点F．将直线向右平移，设平移距离BE为 (t
0)，直角梯形ABCD被直线扫过的面积（图中阴影部份）为S，S关于的函数图象如图②所示，OM为线段，MN为抛物线的一部分，NQ为射线，N点横坐标为4．
信息读取
(1)梯形上底的长AB=；
(2) 直角梯形ABCD的面积=；
图象理解
(3)写出图②中射线NQ表示的实际意义；
(4) 当
时，求S关于的函数关系式；
问题解决
(5)当t为何值时，直线l将直角梯形ABCD分成的两部分面积之比为1: 3．
(1)如图1，OA、OB是⊙O的半径，且OA⊥OB，点C是OB延长线上任意一点，过点C作CD切⊙O于点D，连结AD交DC于点E．则CD=CE吗？如成立，试说明理由。
(2)若将图中的半径OB所在直线向上平行移动交OA于F，交⊙O于B’，其他条件不变，如图2，那么上述结论CD=CE还成立吗?为什么?
(3)若将图中的半径OB所在直线向上平行移动到⊙O外的CF，点E是DA的延长线与CF的交点，其他条件不变，如图3，那么上述结论CD=CE还成立吗?为什么
如图，某人在山坡坡脚A处测得电视塔尖点C的仰角为60°，沿山坡向上走到P处再测得点C的仰角为45°，已知OA=100米，山坡坡度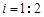
且O,A,B在同一条直线上．求电视塔OC的高度以及此人所在位置P的铅直高度PB．（测倾器高度忽略不计，结果保留根号形式）
甲、乙两超市（大型商场）同时开业，为了吸引顾客，都举行有奖酬宾活动：凡购物满100元，均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球，除颜色外其它都相同，摸奖者一次从中摸出两个球，根据球的颜色决定送礼金券（在他们超市使用时，与人民币等值）的多少（如下表）．
（1）用树状图表示得到一次摸奖机会时摸出彩球的所有情况；
（2）如果只考虑中奖因素，你将会选择去哪个超市购物？请说明理由．
如图，在平面直角坐标系xOy中，矩形OEFG的顶点E的坐标为(4，0)，顶点G的坐标为(0，2)，将矩形OEFG绕点O逆时针旋转，使点F落在y轴的点N处，得到矩形OMNP，OM与GF交于点A．
(1)判断△OGA和△OMN是否相似，并说明理由；
(2)求图象经过点A的反比例函数的解析式；
(3)设(2)中的反比例函数图象交EF于点B，求直线AB的解析式．