已知函数 (
( ,
, 为自然对数的底数).
为自然对数的底数).
(1)求函数 的最小值;
的最小值;
(2)若 ≥0对任意的
≥0对任意的 恒成立,求实数
恒成立,求实数 的值;
的值;
(3)在(2)的条件下,证明:
设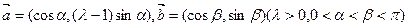 是平面上的两个向量,且
是平面上的两个向量,且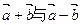 互相垂直.
互相垂直.
(1)求λ的值;
(2)若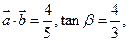 求
求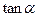 的值.
的值.
已知函数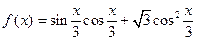 .
.
(I)将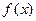 写成
写成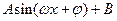 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(II)如果△ABC的三边a、b、c满足b2= a c,且边b所对的角为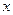 ,试求
,试求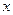 的范围及此时函数
的范围及此时函数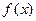 的值域.
的值域.
在东西方向直线延伸的湖岸上有一港口O,一艘机艇以40km/h的速度从O港出发,先沿东偏北的某个方向直线前进到达A处,然后改向正北方向航行,总共航行30分钟因机器出现故障而停在湖里的P处,由于营救人员不知该机艇的最初航向及何时改变的航向,故无法确定机艇停泊的准确位置,试划定一个最佳的弓形营救区域(用图形表示),并说明你的理由.
已知在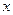 轴上有一点列:
轴上有一点列: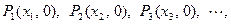
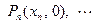 ,点
,点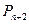 分有向线段
分有向线段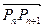 所成的比为
所成的比为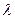 ,其中
,其中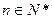 ,
,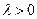 为
为
常数,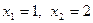 .
.
(1)设 ,求数列
,求数列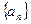 的通项公式;
的通项公式;
(2)设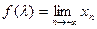 ,当
,当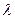 变化时,求
变化时,求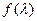 的取值范围.
的取值范围.
在四棱锥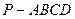 中,
中, ,
, ,
, 底面
底面 ,
,  ,直线
,直线 与底面
与底面 成
成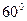 角,点
角,点 分别是
分别是 的中点.
的中点.
(1)求二面角 的大小;
的大小;
(2)当 的值为多少时,
的值为多少时,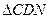 为直角三角形.
为直角三角形.