己知f（x）是定义在R上的增函数，函数y=f（x-l）的图象关于点（1，0）对称，若对任意的x，y∈R，不等式f（x2-6x+21）+f（y2-8y）<0恒成立，则当x>3时，x2+y2的取值范围是（）
| A．（3,7） | B．（9,25） | C．（13,49] | D．（9,49） |
设函数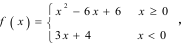
若互不相等的实数x1，x2，x3满足
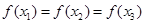，则x1+x2+x3的取值范围是（）
A． |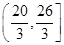
B． |
C． |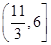
D． |
设函数f’（x）是奇函数f（x）（x∈R）的导函数，f（-1）=0，当x>0时，xf’（x）-f（x）<0，则使得f（x）>0成立的x的取值范围是（）
A．（一∞，一1） （0，1） |
| B．（一1，0）（1，+∞） |
| C．（一∞，一1）（一1，0） |
| D．（0，1）（1，+∞） |
设函数
则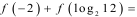
| A．3 | B．6 | C．9 | D．12 |
已知
，则
（）
A． |
B． |
C． |
D． |
成等差数列”是“
”成立的