已知在直角坐标平面内,以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,点 的极坐标是
的极坐标是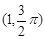 ,曲线C的极坐标方程为
,曲线C的极坐标方程为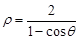 .
.
(I)求点 的直角坐标和曲线C的直角坐标方程;
的直角坐标和曲线C的直角坐标方程;
(II)若经过点 的直线
的直线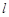 与曲线C交于A、B两点,求
与曲线C交于A、B两点,求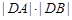 的最小值.
的最小值.
(本小题满分14分)已知函数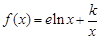 (其中e是自然对数的底数,k为正数)
(其中e是自然对数的底数,k为正数)
(1)若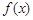 在
在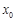 处取得极值,且
处取得极值,且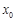 是
是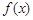 的一个零点,求k的值;
的一个零点,求k的值;
(2)若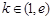 ,求
,求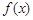 在区间
在区间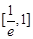 上的最大值.
上的最大值.
(本小题满分13分)如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图的侧视图,俯视图,在直观图中,M是BD的中点,N是BC的中点,侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.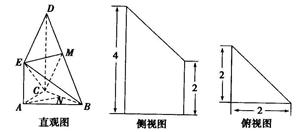
(1)求该几何体的体积;
(2)求证:AN∥平面CME;
(3)求证:平面BDE⊥平面BCD
(本小题满分12分)已知命题P:函数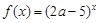 是R上的减函数,命题Q:在
是R上的减函数,命题Q:在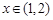 时,不等式
时,不等式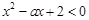 恒成立,若命题“
恒成立,若命题“ ”是真命题,求实数
”是真命题,求实数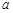 的取值范围.
的取值范围.
(本小题满分12分)已知数列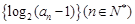 为等差数列,且
为等差数列,且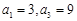
(1)求数列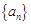 的通项公式;
的通项公式;
(2)证明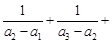 …
…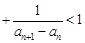 .
.
(本题13分)设椭圆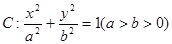 的左右焦点分别为
的左右焦点分别为 ,
,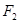 ,上顶点为
,上顶点为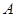 ,过点
,过点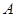 与
与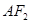 垂直的直线交
垂直的直线交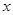 轴负半轴于
轴负半轴于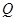 点,且
点,且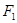 是
是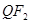 的中点.
的中点.
(1)求椭圆的离心率;
(2)若过点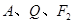 的圆恰好与直线
的圆恰好与直线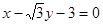 相切,求椭圆
相切,求椭圆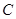 的方程;
的方程;
(3)在(2)的条件下过右焦点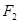 作斜率为
作斜率为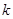 的直线
的直线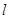 与椭圆相交于
与椭圆相交于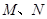 两点,在
两点,在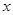 轴上是否存在点
轴上是否存在点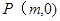 使得以
使得以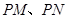 为邻边的平行四边形为菱形,如果存在,求出
为邻边的平行四边形为菱形,如果存在,求出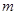 的取值范围,如果不存在,说明理由。
的取值范围,如果不存在,说明理由。