已知在平面直角坐标系中的一个椭圆，它的中心在原点，左焦点为
,且过点
.
（1）求该椭圆的标准方程；
（2）设点
，若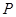
是椭圆上的动点，求线段
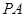的中点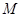
的轨迹方程.
（本小题满分12分 ，要求画图规范）
用平面区域表示不等式组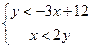
的解集.
（本小题满分12分）已知函数
（
），其中
．
（Ⅰ）当
时，讨论函数
的单调性；
（Ⅱ）若函数仅在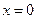
处有极值，求
的取值范围；
（Ⅲ）若对于任意的
，不等式
在
上恒成立，求
的取值范围．
（本小题满分12分）已知
，
，若动点
满足
，点的轨迹为曲线
.
（Ⅰ）求曲线的方程；
（Ⅱ）试确定
的取值范围，使得对于直线
：
，曲线上总有不同的两点关于直线对称.
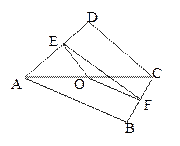
（本小题满分12分）已知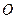
是边长为
的正方形
的中心，点
、
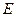分别是
、
的中点，沿对角线
把正方形折成直二面角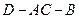
；
（Ⅰ）求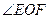
的大小；
（Ⅱ）求二面角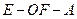
的余弦值；
（Ⅲ）求点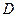
到面
的距离.
（本小题满分12分）求一条渐近线方程是
，且过点
的双曲线的标准方程，并求此双曲线的离心率.