如图1,已知线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;
(2)仔细观察,在图2中“8字形”的个数:个;
(3)在图2中,若∠D=40°,∠B=36°,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠P与∠D、∠B之间数量关系,并说明理由.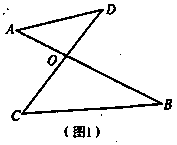

在5×6的方格图中,
在图1中,将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分),
在图2中,将线段A1A2A3向右平移1个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分),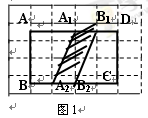
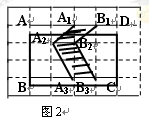
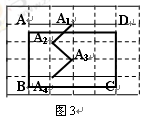
(1)在图3中,画出将折线A1A2A3A4向右平移1单位后的图形,并用阴影画出由这两条折线所围成的封闭图形.
(2)设上述三个图形中,矩形ABCD分别除去阴影部分后剩余部分的面积记为S1、S2、S3,则S1=,S2=,S3=.
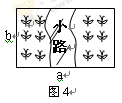
(3)如图4,在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想草地部分的面积是.(用含a、b的代数式表示)
计算图中阴影部分的面积.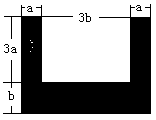
如图,已知AD∥BE,∠1=∠2,试判断∠A和∠E之间的大小关系,并说明理由.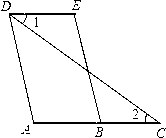
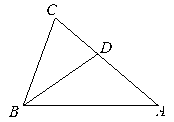
如图,BD是△ABC的角平分线,∠A=40°,∠ABD=35°,求∠C和∠CDB的度数.