一轻质细绳一端系一质量为
的小球A，另一端挂在光滑水平轴O 上，O到小球的距离为L=0.1m，小球跟水平面接触，但无相互作用，在球的两侧等距离处分别固定一个光滑的斜面和一个挡板，如图所示，水平距离s为2m，动摩擦因数为0.25．现有一小滑块B，质量也为m，从斜面上滑下，与小球碰撞时交换速度，与挡板碰撞不损失机械能．若不计空气阻力，并将滑块和小球都视为质点，g取10m/s2，试问：
（1）若滑块B从斜面某一高度h处滑下与小球第一次碰撞后，使小球恰好在竖直平面内做圆周运动，求此高度h.
（2）若滑块B从h=5m处滑下，求滑块B与小球第一次碰后瞬间绳子对小球的拉力．
（3）若滑块B从h="5m" 处下滑与小球碰撞后，小球在竖直平面内做圆周运动，求小球做完整圆周运动的次数n．
A、B两物体（视为质点）在同一直线上同时出发向同一方向运动，物体A从静止开始做匀加速直线运动，加速度的大小a=2m/s2，物体B在A的后面相距L=16m处，以v1=10m/s的速度做匀速运动。两物体追逐时，互从近旁通过，不会相碰。
求：经过多长时间物体B追上物体A？
共经过多长时间A、B两物体再次相遇？
A、B两物体两次相遇之间相距最远的距离是多少？
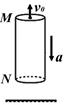
如下图所示，离地面足够高处有一竖直的空心管，质量为2kg，管长为24m，M、N为空心管的上、下两端，空心管受到大小为16N的竖直向上的拉力作用，由静止开始竖直向下做匀加速运动，同时在M处有一个大小不计的小球沿管的轴线做竖直上抛运动，取g＝10m/s2。若小球上抛的初速度为10m/s，试问：经过多少秒小球从管的N端穿出。
若此空心管的N端距离地面高为64m，欲使在空心管到达地面时小球刚好进入管内，在其他条件不变的前提下，则小球初速度大小应为多大？
2010年11月22日晚短跑名将劳义在广州亚运会上创造了100m亚洲纪录，他的成绩是10.24s，劳义在短跑项目上有过人的天赋，100米，200米都是他的强项，200米在训练时也能达到20.34秒的好成绩，据悉他下一步训练将侧重200米的训练，比赛时从发令到起跑的反应时间是0.15s，起跑后做匀加速运动，达到最大速率后做匀速运动。200m比赛时，反应时间及起跑后加速阶段的加速度和加速时间与l00m比赛时相同，但由于弯道和体力等因素的影响，以后的平均速率只有跑l00m时最大速率的96%。（结果保留两位小数）
求：加速所用时间和达到的最大速率；
起跑后做匀加速运动的加速度。
2010年4月22日14时43分，某记者从厦门火车站的1号站台上了一列和谐号动车，提前体验福厦高铁的高速。该记者记录了如下数据：动车从静止开始启动经过时间280s达到速率为70m/s，并以此速率连续运行了1小时后开始减速进福州站，又经过280s停靠在站台旁。设动车加速与减速阶段都做匀变速直线运动。
试求：动车在加速过程的加速度为多少？
厦门站到福州站的总路程为多少？
某宇航员在飞船发射前测得自身连同宇航服等随身装备共重840 N,在火箭发射阶段,发现当飞船随火箭以a=g/2的加速度匀加速竖直上升到某位置时(其中g为地球表面处的重力加速度),其身下体重测试仪的示数为1220 N.设地球半径R="6400" km,地球表面重力加速度g="10" m/s2(求解过程中可能用到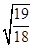
=1.03，
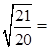1.02).问:该位置处的重力加速度g′是地面处重力加速度g的多少倍?
该位置距地球表面的高度h为多大?