某商品的进价为每件40元，售价为每件50元，每个月可卖出210件；如果每件商品在该售价的基础上每上涨1元，则每个月少卖10件（每件售价不能高于65元）．设每件商品的售价上涨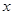
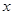元（为正整数），每个月的销售利润为
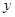元．(14分)
（1）求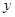与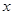的函数关系式并直接写出自变量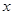的取值范围；
（2）每件商品的售价定为多少元时，每个月可获得最大利润？最大的月利润是多少元？
判断下列问题是排列问题还是组合问题？并计算出结果.
高二年级数学课外小组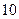
人：①从中选一名正组长和一名副组长，共有多少种不同的选法？②从中选
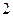名参加省数学竞赛，有多少种不同的选法？
判断下列问题是排列问题还是组合问题？并计算出结果.
高三年级学生会有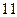
人：①每两人互通一封信，共通了多少封信？②每两人互握了一次手，共握了多少次手？
是否存在正方形ABCD，它的对角线AC在直线x+y-2=0上，顶点B、D在抛物线y2=4x上?若存在，试求出正方形的边长；若不存在，试说明理由.
抛物线y=-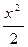
与过点M(0，-1)的直线l相交于A、B两点，O为坐标原点，若直线OA和OB斜率之和为1，求直线l的方程.
已知圆C过定点A(0，p)(p＞0)，圆心C在抛物线x2=2py上运动，若MN为圆C在x轴上截得的弦，设｜AM｜=m,｜AN｜=n，∠MAN=θ.
(1)当点C运动时，｜MN｜是否变化?写出并证明你的结论?
(2)求
+
的最大值，并求取得最大值时θ的值和此时圆C的方程.若不存在，说明理由