ABCD为平行四边形,P为平面ABCD外一点,PA⊥面ABCD,且PA=AD=2,AB=1,AC=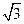 。
。
求证:平面ACD⊥平面PAC;
求异面直线PC与BD所成角的余弦值;
设二面角A—PC—B的大小为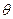 ,试求
,试求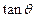 的值。
的值。
已知函数
(1)求函数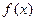 的最小正周期;
的最小正周期;
(2)若对任意的x∈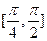 ,不等式f(x)>m-3恒成立,求实数m的取值范围.
,不等式f(x)>m-3恒成立,求实数m的取值范围.
在三角形ABC中,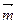 =(cos
=(cos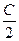 ,sin
,sin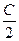 ),
), 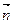 =(cos
=(cos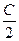 ,-sin
,-sin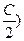 且
且 的夹角为
的夹角为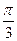
(1)求C;
(2)已知c=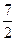 ,三角形的面积S=
,三角形的面积S=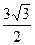 ,求a+b(a、b、c分别∠A、∠B、∠C所对的边)
,求a+b(a、b、c分别∠A、∠B、∠C所对的边)
在△ABC中,A、B、C的对边分别是a、b、c,且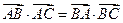
(1)判断△ABC的形状;
(2)若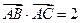 ,求边c的值.
,求边c的值.
某单位在抗雪救灾中,需要在A、B两地之间架设高压电线,测量人员在相距6000m的C、D两地(A、B、C、D在同一平面上),测得∠ACD=45°,∠ADC=75°,∠BCD=30°,∠BDC=15°(如图),假如考虑到电线的自然下垂和施工损耗等原因,实际所须电线长度大约应该是A、B距离的1.2倍,问施工单位至少应该准备多长的电线?(参考数据: )
)
已知函数 ,
,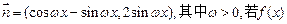 相邻两对称轴间的距离大于等于
相邻两对称轴间的距离大于等于
(Ⅰ)求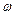 的取值范围;
的取值范围;
(Ⅱ)在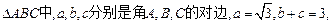
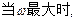
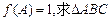 的面积.
的面积.