已知某几何体的直观图和三视图如图所示,其正(主)视图为矩形,侧(左)视图为等腰直角三角形,俯视图为直角梯形.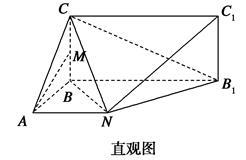
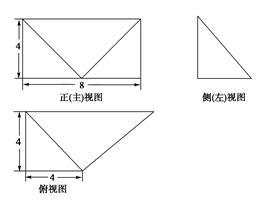
(1)若M为CB中点,证明:MA∥平面CNB1;
(2)求这个几何体的体积.
已知函数 ,
, (其中
(其中 ).
).
(Ⅰ)如果函数 和
和 有相同的极值点,求
有相同的极值点,求 的值,并直接写出函数
的值,并直接写出函数 的单调区间;
的单调区间;
(Ⅱ)求方程 在区间
在区间 上实数解的个数.
上实数解的个数.
已知两点 、
、 ,动点
,动点 与
与 、
、 两点连线的斜率
两点连线的斜率 、
、 满足
满足 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ) 是曲线
是曲线 与
与 轴正半轴的交点,曲线
轴正半轴的交点,曲线 上是否存在两点
上是否存在两点 、
、 ,使得
,使得 是以
是以 为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
已知各项均为正数的数列 的前
的前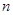 项和为
项和为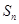 ,且
,且 (
(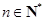 ).
).
(Ⅰ)求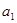 的值及数列
的值及数列 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前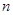 项和为
项和为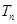 ,求证:
,求证: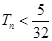 (
(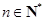 );
);
如图,三棱柱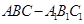 中,
中, ,
, ,平面
,平面 平面
平面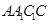 ,
,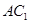 与
与 相交于点
相交于点 .
.
(Ⅰ)求证: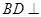 平面
平面 ;
;
(Ⅱ)求二面角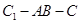 的余弦值.
的余弦值.
某中学校本课程共开设了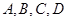 共
共 门选修课,每个学生必须且只能选修
门选修课,每个学生必须且只能选修 门选修课,现有该校的甲、乙、丙
门选修课,现有该校的甲、乙、丙 名学生.
名学生.
(Ⅰ)求这 名学生选修课所有选法的总数;
名学生选修课所有选法的总数;
(Ⅱ)求恰有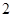 门选修课没有被这
门选修课没有被这 名学生选择的概率;
名学生选择的概率;
(Ⅲ)求 选修课被这
选修课被这 名学生选择的人数
名学生选择的人数 的分布列和数学期望.
的分布列和数学期望.