(本小题满分12分)
已知数列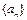 的首项
的首项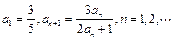 .
.
(Ⅰ)求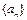 的通项公式;
的通项公式;
(Ⅱ)证明:对任意的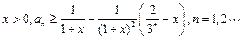 ;
;
(Ⅲ)证明: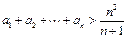 .
.
(本小题满分12分)
己知双曲线的中心在原点,右顶点为
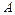 (1,0),点
(1,0),点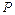 .Q在双曲线的右支上,点
.Q在双曲线的右支上,点 (
(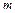 ,0)到直线
,0)到直线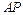 的距离为1.
的距离为1.
(Ⅰ)若直线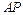 的斜率为
的斜率为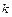 且有
且有 ,求实数
,求实数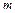 的取值范围;
的取值范围;
(Ⅱ)当 时,
时,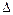
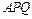 的内心恰好是点
的内心恰好是点 ,求此双曲线的方程.
,求此双曲线的方程.
.(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是一直角梯形,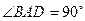 ,AD//BC, AB=
,AD//BC, AB= BC=1,AD=2,PA
BC=1,AD=2,PA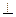 底面ABCD,PD与底面成
底面ABCD,PD与底面成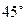 角,点E是PD的中点.
角,点E是PD的中点.
(1)求证:BE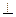 PD;
PD;
(2)求二面角P-CD-A的余弦值.
(本小题满分12分)
某超市为了响应环保要求,鼓励顾客自带购物袋到超市购物,采取了如下措施:对不使用超市塑料购物袋的顾客,超市给予0.96折优惠;对需要超市塑料购物袋的顾客,既要付购买费,也不享受折扣优惠.假 设该超市在某个时段内购物的人数为36人,其中有12位顾客自己带了购物袋,现从这36人中随机抽取2人.
设该超市在某个时段内购物的人数为36人,其中有12位顾客自己带了购物袋,现从这36人中随机抽取2人.
(Ⅰ)求这2人都享受折扣优惠或都不享受折扣优惠的概率;
(Ⅱ)设这2人中享受折扣优惠的人数为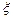 ,求
,求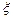 的分布列和数学期望.
的分布列和数学期望.
(本小题满分10分)
已知函数
(Ⅰ)将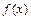 写成
写成 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(Ⅱ)如果△ABC的三边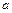 ,
, ,
, 满足
满足 ,且边
,且边 所对的角为
所对的角为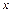 ,试求角
,试求角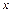 的范围及函数
的范围及函数
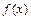 的值域.
的值域.