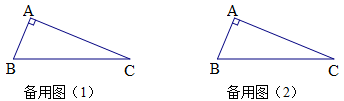如图,抛物线y=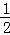 x2﹣
x2﹣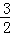 x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
x﹣9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.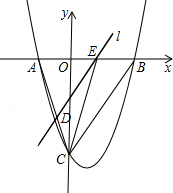
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).
(1)若a与2b互为倒数,-c与 互为相反数,
互为相反数, =3,求2ab-2c+d+
=3,求2ab-2c+d+ 的值.
的值.
(2)已知当x=2时,代数式ax3-bx+1的值为-17,求当x=-1时,代数式12ax-3bx3-5的值是多少?
化简:①x-2[y+2x―(3x―y)];
② m―2(m―
m―2(m― n2)―(
n2)―( m―
m― n2);
n2);
③ 先化简,再求值:2(a2b+ab2)―3(a2b―1)―2ab2―4,其中a=2014,b= .
.
(1)如图,两个圈分别表示负数集和分数集,请将3,0, ,
, ,-5,-3.4中,符合要求的数填入相应的圈中;
,-5,-3.4中,符合要求的数填入相应的圈中;
(2)在数轴上表示下列四个数-2, ,0,
,0, ,并把它们用“<”号连接起来.
,并把它们用“<”号连接起来.
如图,在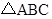 中,
中, ,
,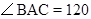 °,
°,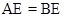 ,
, 为
为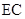 中点.
中点.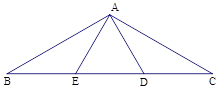
(1)求 的度数;
的度数;
(2)求证: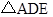 是等边三角形
是等边三角形
已知在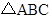 中,
中,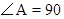 °,
°,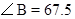 °,请画出一条直线,把这个三角形分割成两个等腰三角形(请你选用下面给出的备用图,把所有不同的分割方法都画出来,只需画图,不必说明理由,但要在图中标出相等两角的度数)
°,请画出一条直线,把这个三角形分割成两个等腰三角形(请你选用下面给出的备用图,把所有不同的分割方法都画出来,只需画图,不必说明理由,但要在图中标出相等两角的度数)