已知:如图1,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ. 若设运动的时间为t(s)( 0<t<2 ),解答下列问题: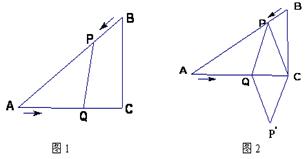
(1)t为何值时,PQ∥BC?
(2)设△AQP的面积为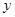 (
(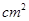 ),求
),求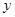 与t之间的函数关系;
与t之间的函数关系;
(3)是否存在某一时刻t,使线段PQ恰好把Rt△ACB的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;
(4)如图2,连接PC,并把△PQC沿QC翻折,得到四边形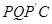 ,那么是否存在t,使四边形
,那么是否存在t,使四边形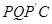 为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为菱形?若存在,求出此时菱形的边长;若不存在,说明理由.
为调查达州市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“ :自行车, :电动车, :公交车, :家庭汽车, :其他”五个选项中选择最常用的一项.将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
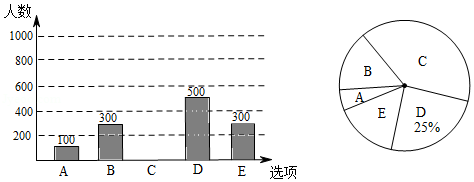
(1)本次调查中,一共调查了 2000 名市民;扇形统计图中, 项对应的扇形圆心角是 度;补全条形统计图;
(2)若甲、乙两人上班时从 、 、 、 四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.
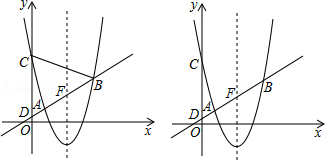
如图,在平面直角坐标系 中,以直线 对称轴的抛物线 与直线 交于 , 两点,与 轴交于 ,直线 与 轴交于点 .
(1)求抛物线的函数表达式;
(2)设直线 与抛物线的对称轴的交点为 , 是抛物线上位于对称轴右侧的一点,若 ,且 与 面积相等,求点 的坐标;
(3)若在 轴上有且仅有一点 ,使 ,求 的值.
在 中, , , ,过点 作直线 ,将 绕点 顺时针旋转得到△ (点 , 的对应点分别为 , ,射线 , 分别交直线 于点 , .
(1)如图1,当 与 重合时,求 的度数;
(2)如图2,设 与 的交点为 ,当 为 的中点时,求线段 的长;
(3)在旋转过程中,当点 , 分别在 , 的延长线上时,试探究四边形 的面积是否存在最小值.若存在,求出四边形 的最小面积;若不存在,请说明理由.

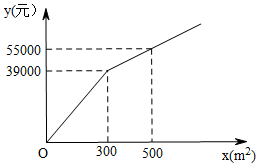
为了美化环境,建设宜居成都,我市准备在一个广场上种植甲、乙两种花卉,经市场调查,甲种花卉的种植费用 (元 与种植面积 之间的函数关系如图所示,乙种花卉的种植费用为每平方米100元.
(1)直接写出当 和 时, 与 的函数关系式;
(2)广场上甲、乙两种花卉的种植面积共 ,若甲种花卉的种植面积不少于 ,且不超过乙种花卉种植面积的2倍,那么应该怎样分配甲、乙两种花卉的种植面积才能使种植总费用最少?最少总费用为多少元?
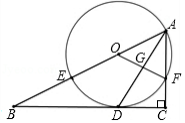
如图,在 中, , 平分 交 于点 , 为 上一点,经过点 , 的 分别交 , 于点 , ,连接 交 于点 .
(1)求证: 是 的切线;
(2)设 , ,试用含 , 的代数式表示线段 的长;
(3)若 , ,求 的长,