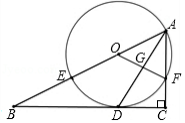
如图,在 中, , 平分 交 于点 , 为 上一点,经过点 , 的 分别交 , 于点 , ,连接 交 于点 .
(1)求证: 是 的切线;
(2)设 , ,试用含 , 的代数式表示线段 的长;
(3)若 , ,求 的长,
如图,已知二次函数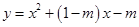 (其中0<m<1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC.
(其中0<m<1)的图像与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.设P为对称轴l上的点,连接PA、PC,PA=PC. 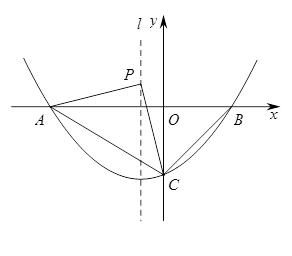
(1)∠ABC的度数为°;
(2)求P点坐标(用含m的代数式表示);
(3)在坐标轴上是否存在点Q(与原点O不重合),使得以Q、B、C为顶点的三角形与△PAC相似,且线段PQ的长度最小?如果存在,求出所有满足条件的点Q的坐标;如果不存在,请说明理由.
如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点,过点B作BE∥AD,交⊙O于点E,连接ED.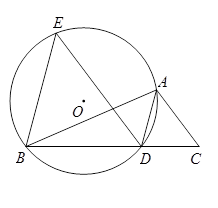
(1)求证:ED∥AC;
(2)若BD=2CD,设△EBD的面积为 ,△ADC的面积为
,△ADC的面积为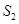 ,且
,且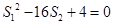 ,求△ABC的面积.
,求△ABC的面积.
如图,已知函数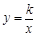 (x>0)的图像经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图像经过点A、D,与x轴的负半轴交于点E.
(x>0)的图像经过点A、B,点B的坐标为(2,2).过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,AC与BD交于点F.一次函数y=ax+b的图像经过点A、D,与x轴的负半轴交于点E.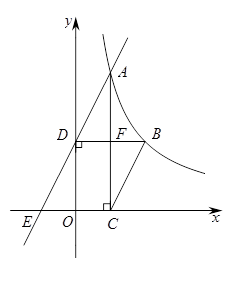
(1)若AC=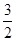 OD,求a、b的值;
OD,求a、b的值;
(2)若BC∥AE,求BC的长.
如图,在△ABC中,AB=AC.分别以B、C为圆心,BC长为半径在BC下方画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD、BD、CD.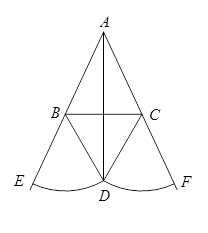
(1)求证:AD平分∠BAC;
(2)若BC=6,∠BAC=50°,求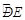 、
、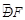 的长度之和(结果保留
的长度之和(结果保留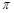 ).
).
一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.