如图,双曲线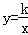 (x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
(x>0)上有一点A(1,5),过点A的直线y=mx+n与x轴交于点C(6,0).
(1)求反比例函数和一次函数的解析式;
(2)连接OA、OB,求△AOB的面积;
(3)根据图象直接写出在第一象限内反比例函数值大于一次函数值时x的取值范围.
(1)如图所示,如果你的位置在点A,你能看到后面那座高大的建筑物吗?为什么?
(2)如果两楼之间相距MN=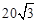 m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?
m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?
计算下列各题:
(1) (2)
(2)
平面直角坐标系xOy中,抛物线y=ax2-4ax+4a+c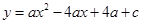 与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
与x轴交于点A、B,与y轴的正半轴交于点C,点A的坐标为(1,0),OB=OC.
(1)求此抛物线的解析式;
(2)若点P是线段BC上的一个动点,过点P作y轴的平行线与抛物线在x轴下方交于点Q,试问线段PQ的长度是否存在最大值?若存在,求出其最大值;若不存在,请说明理由;
(3)若此抛物线的对称轴上的点M满足∠AMC=45°,求点M的坐标.
如图,AB是⊙O的直径,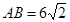 ,M是弧AB的中点,OC⊥OD,△COD绕点O旋转与△AMB的两边分别交于E、F(点E、F与点A、B、M均不重合),与⊙O分别交于P、Q两点.
,M是弧AB的中点,OC⊥OD,△COD绕点O旋转与△AMB的两边分别交于E、F(点E、F与点A、B、M均不重合),与⊙O分别交于P、Q两点.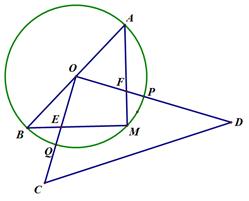
(1)求证: ;
;
(2)连接PM、QM,试探究:在△COD绕点O旋转的过程中,∠PMQ是否为定值?若是,求出∠PMQ的大小;若不是,请说明理由;
(3)连接EF,试探究:在△COD绕点O旋转的过程中,△EFM的周长是否存在最小值?若存在,求出其最小值;若不存在,请说明理由
如图,一架长2.5米的梯子AB斜靠在竖直的墙AC上,这时B到墙AC的距离为0.7米.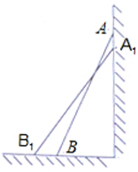
(1)若梯子的顶端A沿墙AC下滑0.9米至A1处,求点B向外移动的距离BB1的长;
(2)若梯子从顶端A处沿墙AC下滑的距离是点B向外移动的距离的一半,试求梯子沿墙AC下滑的距离是多少米?