如图1，是一个长为2m、宽为2n的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后按图2的形状拼成一个正方形．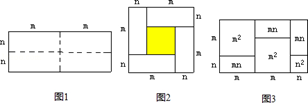
（1）图2中阴影部分的面积为 （m﹣n）2 ；
（2）观察图2，请你写出三个代数式（m+n）2、（m﹣n）2、mn之间的等量关系式： （m﹣n）2+4mn=（m+n）2 ；
（3）根据（2）中的结论，若x+y=﹣6，xy=2.75，则x﹣y= ±5 ．
（4）有许多代数恒等式可以用图形的面积来表示．如图3，它表示了（2m+n）（m+n）=2m2+3mn+n2．试画出一个几何图形，使它的面积能表示（m+n）（m+3n）=m2+4mn+3n2．
证明命题“等腰三角形底边上的中点到两腰的距离相等”。(要求画图，写已知 求证和证明)
为了帮助贫困失学儿童重返学校，某校发起参加“爱心储蓄”活动，鼓励学生将自己的压岁钱、零用钱存入银行，定期一年，到期后可取回本金，而把利息捐给贫困儿童。该校共有学生1200人，下列两个图为该校各年级学生人数比例分布情况图和学生人均存款情况图。
(1)该校九年级学生存款总数为元；
(2)该校学生的人均存款额为多少元?
(3)已知银行一年期定期存款的年利率为2．25％(“爱心储蓄”免征利息税)，且每35l元能够提供一位失学儿童一学年的基本费用。那么该校一年能够帮助多少名贫困失学儿童? 
已知二次函数
.
(1).求出该函数图象的顶点坐标，对称轴，并在右侧的网格中画出这个函数的大致图象。
(2)利用函数图象回答：当x在什么范围内时,y>0?
如图所示，已知在梯形ABCD中，AD∥BC，∠ABC=60°，BD平分∠ABC，且BD⊥DC．
求证：梯形ABCD是等腰梯形
如图，在△ABC中，∠C＝90º，AC＝6cm，BC＝8cm，D、E分别是AC、AB
的中点，连接DE．点P从点D出发，沿DE方向匀速运动，速度为1cm/s；同时，点Q从点B出发，沿
BA方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t(0＜t
＜4)s．解答下列问题：
(1)当t为何值时，PQ⊥AB？
(2)当点Q在B、E之间运动时，设五边形PQBCD的面积为ycm2，求y与t之间的函数关系式；
(3)在(2)的情况下，是否存在某一时刻t，使得PQ分四边形BCDE所成的两部分的面积之比为
＝1∶29？若存在，求出此时t的值以及点E到PQ的距离h；若不存在，请说明理由．