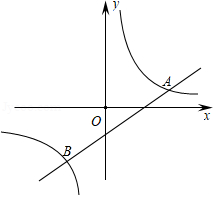
在△ABC中,∠BAC=90°,AB<AC,M是BC边的中点,MN⊥BC交AC于点N.动点P从点B出发沿射线BA以每秒 厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ丄MP.设运动时间为t秒(t>0).
厘米的速度运动.同时,动点Q从点N出发沿射线NC运动,且始终保持MQ丄MP.设运动时间为t秒(t>0).
(1)△PBM与△QNM相似吗?以图1为例说明理由:
(2)若∠ABC=60°,AB=4 厘米.
厘米.
①求动点Q的运动速度;
②设△APQ的面积为S(平方厘米),求S与t的函数关系式.
如图,顶点为 的二次函数图象与 轴交于点 ,点 在该图象上, 交其对称轴 于点 ,点 、 关于点 对称,连接 、 .
(1)求该二次函数的关系式.
(2)若点 在对称轴 右侧的二次函数图象上运动,请解答下列问题:
①连接 ,当 时,请判断 的形状,并求出此时点 的坐标.
②求证: .
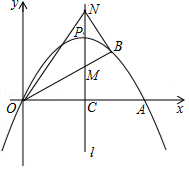
如图, 内接于 ,直径 交 于点 ,延长 至点 ,使 ,连接 并延长交过点 的切线于点 ,且满足 ,连接 ,若 , .
(1)求证: ;
(2)求 的半径 ;
(3)求证: 是 的切线.
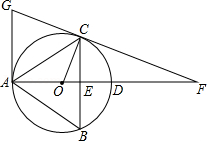
如图,一次函数 的图象与反比例函数 的图象交于点 与点 .
(1)求反比例函数的表达式;
(2)若动点 是第一象限内双曲线上的点(不与点 重合),连接 ,且过点 作 轴的平行线交直线 于点 ,连接 ,若 的面积为3,求出点 的坐标.
我市某校为了让学生的课余生活丰富多彩,开展了以下课外活动:
|
代号 |
活动类型 |
|
|
经典诵读与写作 |
|
|
数学兴趣与培优 |
|
|
英语阅读与写作 |
|
|
艺体类 |
|
|
其他 |
为了解学生的选择情况,现从该校随机抽取了部分学生进行问卷调查(参与问卷调查的每名学生只能选择其中一项),并根据调查得到的数据绘制了如图所示的两幅不完整的统计图.请根据统计图提供的信息回答下列问题(要求写出简要的解答过程).
(1)此次共调查了 名学生.
(2)将条形统计图补充完整.
(3)“数学兴趣与培优”所在扇形的圆心角的度数为 .
(4)若该校共有2000名学生,请估计该校喜欢 、 、 三类活动的学生共有多少人?
(5)学校将从喜欢“ ”类活动的学生中选取4位同学(其中女生2名,男生2名)参加校园“金话筒”朗诵初赛,并最终确定两名同学参加决赛,请用列表或画树状图的方法,求出刚好一男一女参加决赛的概率.

仙桃是遂宁市某地的特色时令水果.仙桃一上市,水果店的老板用2400元购进一批仙桃,很快售完;老板又用3750元购进第二批仙桃,所购件数是第一批的 倍,但进价比第一批每件多了5元.
(1)第一批仙桃每件进价是多少元?
(2)老板以每件225元的价格销售第二批仙桃,售出 后,为了尽快售完,剩下的决定打折促销.要使得第二批仙桃的销售利润不少于2460元,剩余的仙桃每件售价至少打几折?(利润 售价 进价)